 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Виды математических моделей
В зависимости от характера отношений между элементами моделируемых объектов (процессов или явлений) различают метрические и неметрические математические модели. В свою очередь метрические модели могут быть: динамические или статические, детерминированные или вероятностные. Статические модели используются для описания объектов в определённый момент времени, в динамических моделях переменные зависят от непрерывно и равномерно изменяющегося аргумента (чаще всего времени). В качестве статических моделей чаще всего используются числовые функции, например, в экономике зависимость спроса и предложения от цены на товар может выражаться как линейной, так и квадратичной функцией. Наглядные и многочисленные примеры описания процессов, зависящих от времени, дает классическая механика. Для исследования динамических моделей наилучшим оказался аппарат дифференциальных уравнений. Динамические модели широко используются при расчете орбит спутников и траекторий ракет в задачах земной и небесной механики. При надлежащей информации эти модели дают совершенно определенные и однозначные предсказания. Модель детерминированная, если каждому входному набору параметров соответствует вполне определенный и однозначно определяемый набор выходных параметров, в противном случае модель недетерминированная, стохастическая (вероятностная). Так как в реально существующих технических природных системах часто имеют место случайные, «вероятностные» отношения, то метрические стохастические модели разрабатываются с помощью теории вероятностей. Практика показала, что системы, в которых соотношения между переменными являются случайными, не менее многочисленны, чем детерминированные системы, кроме того, выяснилось, что почти в каждой изучаемой реальной ситуации присутствует элемент случайности. Физическая модель свободного падения тела S=gt2/2 при tÎ(0,100) пример детерминированной модели, однако если в ней учесть случайный параметр – порыв ветра с силой p при падении тела, например, S(р)=g(р)t2/2 при tÎ(0,100), то получим уже стохастическую модель (уже не свободного) падения. Предсказания, получаемые с помощью статистических моделей, имеют вероятностный характер. Такого вида модели применяются там, где приходится учитывать совокупное действие огромного числа частиц или факторов, например, в квантовой механике при изучении закономерностей движения мельчайших частиц материи – атомов, электронов, протонов и т.д. Примером «вероятностной модели вероятностной системы» может служить современная теория массового обслуживания. Модели этого вида применяются не только в физике и экономике, но и в биологии, социологии. Как видно из приведенного выше примера, распределение метрических моделей на указанные виды не является абсолютным. Предельным переходом из вероятностных моделей получаются динамические, а из динамических – вероятностные. В 17, 18 и первой половине 19 века математические модели реальных явлений почти всегда строились, исходя из принципа полной детерминированности их протекания (то есть из предположения, что каждое состояние в данный момент времени приводит к одному определенному состоянию в каждый заданный последующий момент). Таковы модели классической механики, оптики, гидродинамики и многих других областей знания. Однако уже с середины 17 века в науке стали пробиваться идеи статистических моделей. Сначала были изучены демографические явления, такие как смертность, рождаемость, выздоровление от заразных заболеваний и пр. Здесь уже представление о полной детерминированности явлений не находило подтверждений, и для их количественного изучения необходимо было разработать новые математические методы исследования. Это были методы теории вероятностей и зарождающейся математической статистики. В середине 18 века в связи, главным образом, с успехами астрономии возник вопрос о закономерностях, с которыми приходится иметь дело при рассмотрении погрешности наблюдений. Этой задачей занимались многие крупные математики того времени; решение было найдено почти одновременно французским математиком Лежандром и немецким ученым Гауссом в 1809 г. Особенно быстро пошло развитие статистических моделей в естествознании со второй половины 20 века, когда Масквеллом, Больцманом и другими исследователями была построена кинетическая теория газов, основанная на гипотезе, что любой газ состоит из большого числа молекул, находящихся в непрестанном движении. С 10-х годов 20 столетия началось применение теории вероятностей к задачам телефонии. Возникновение новых математических методов и попытки применить их в таких науках как биология, психология, социология привели к созданию неметрическихмоделей. Эти модели отображают неметрические характеристики и отношения, для их построения используются алгебраические, теоретико-множественные методы, а также понятия и методы теории графов. Модель теоретико-множественная, если она представима с помощью некоторых множеств и отношений принадлежности им и между ними. Пример такой модели. Пусть задано множество Х={Николай, Петр, Елена, Михаил, Татьяна, Ольга} и отношения: Николай – супруг Елены, Ольга – супруга Петра, Михаил – сын Николая и Елены, Татьяна – дочь Петра и Ольги, семьи Николая и Петра дружат друг с другом. Тогда множество Х и множество перечисленных отношений У могут служить теоретико-множественной моделью двух дружественных семей. К неметрическим моделям относятся логические модели, которые представимы предикатами, логическими функциями. Например, совокупность двух логических функций вида В зависимости от назначения математические модели можно разделить на · Дескриптивные (от англ. описание) модели разрабатываются для описания реально существующих процессов, объектов без вмешательства в них (их часто называют моделями без управления). Они создаются для принятия различных управленческих решений, но в самой модели не предусматривается выбор количественно обоснованного решения с позиции какого-то определенного критерия эффективности. Их используют для прогнозирования различных социальных явлений (например, преступности). Они обычно отвечают на вопросы: как будет, как есть сейчас; дают общее представление о системе, объекте и применяются для изучения только самых общих изменений и тенденций. · Оптимизационные – модели, используемые в управлении процессами, позволяющие находить экстремальное значение одной целевой функции. Они ориентированы на решение практических задач совершенствования управления социально-правовыми, экономическими и другими системами. Отличительной их чертой является наличие четкого целенаправленного решения, критерия эффективности для оценки решений и выбор из них оптимального. Такие модели помогают ответить на вопрос: как должно быть? · Многокритериальные – модели, которые позволяют находить экстремальное значение нескольких целевых функций; · Игровые – модели, используемые в ситуациях, когда участники процесса (например, игры) имеют не совпадающие интересы; · Имитационные, используемые для исследования сложных систем, прогнозирования их будущих состояний в зависимости от избираемых стратегий управления. Имитационные модели используют для моделирования больших систем, состоящих из комплекса подсистем с собственными целями, нередко противоречивыми, состояние которых зависит от многих факторов и отличается неопределенностью. При этом возникает ситуация, когда или трудно выделить какой-либо критерий, или имеется несколько противоречивых критериев. Имитационные модели позволяют заранее ответить на вопрос: что будет, если события будут развиваться по тому или иному варианту (сценарию)? Имитация деятельности изучаемой системы, проверка различных вариантов развития (сценариев) и решения осуществляются на компьютерах (машинная имитация) Наиболее просто он решается в случае, когда хорошо известны законы, определяющие поведение и свойства объекта и имеется большой практический опыт их применения. В этом случае можно априори (до опыта) оценить точность результата, которую обеспечивает математическая модель. Таким примером является расчет траектории движения автоматической станции Луна-1 в межпланетном пространстве. (Запуск станции осуществлен 2 января 1959 года). Он проводился на основании математической модели, использующей законы механики и закон всемирного тяготения. Многовековой опыт наблюдения за небесными телами в Солнечной системе показал, что такая модель очень точно описывает их движение В настоящее время математическое моделирование используется и тогда, когда о физической структуре явления известно немного. В этом случае строится гипотетическая модель и на ее основе выводятся следствия, уже доступные наблюдению. Даже если такие модели и не подтверждаются опытом, ценность их несомненна: они активизируют работу мысли, наводят на новые эксперименты, позволяют продвигаться в познании окружающего нас мира. Построенные математические модели подвергаются исследованию. Исследование – это сложный и многосторонний процесс. По выражению Н.Н.Моисеева «любая модель – это некоторая абстракция, звено в цепочке познания – от опыта к абстракции, к осмысливанию открытых явлений и снова к практике, к использованию добытых знаний». Основным характерным признаком исследования математических моделей является применение логических дедукций. Эти дедукции применяются к системе основных понятий, выделенных из реальных объектов. Относительно систем обычно формулируют исходные высказывания, описывающие выделяемые свойства объектов. Модели подвергаются также опытной проверке, в ходе которой проявляется возможность исследовать соответствие каждой из предпосылок реальности. Модель в значительной степени предопределяет то, какими средствами мы должны пользоваться при изучении интересующих нас вопросов. Если в математике не находятся необходимые средства изучения, то их создают заново. Но не каждая модель может быть непосредственно проверена на опыте. Например, первый закон Ньютона принципиально не может быть проверен, так как нигде во Вселенной не существует условий, чтобы на материальное тело не действовали силы. Понимая это трудности, И. Ньютон говорил о мысленном эксперименте. Критерием того, что этот закон справедлив, должны быть результаты использования этого закона в практике людей. Методом исследования математических моделей является вычислительный эксперимент. Вычислительный эксперимент можно считать заключительным этапом математического моделирования. Сравнение его результатов с практическими позволяет либо утвердить модель, либо внести в модель поправки. До появления современных ЭВМ и современных разделов прикладной математики исследования случайных процессов и явлений проводили экспериментальным путем постановки дорогостоящих уникальных опытов. Пусть требуется решить задачу возвращения космического аппарата на Землю. Возникает целый комплекс исследования различных данных: силовые нагрузки на аппарат, тепловой режим и т.д. На данные влияют свойства среды (теплоемкость, теплопроводность и т.д.). Эти свойства зависят от температуры, которая меняется в широком диапазоне из-за сильного разогрева воздуха самим аппаратом. Получить всю нужную информацию путем лабораторного эксперимента невозможно, но такое исследование можно выполнить на ЭВМ с использованием математической модели, представляющей собой взаимосвязанные уравнения аэродинамики, теплопроводности и получить траекторию полета аппарата и всю нужную информацию о его режиме?? В математическом моделировании существуют два направления, взаимно дополняющих друг друга, но преследующих различные цели. Одно направление связано с построением детализированных моделей, в которых исследователь стремится по возможности более подробно изучить различные стороны процесса. При этом модель получается настолько сложной, что численный эксперимент на этой модели представляет собой большую специальную работу, требующую много машинного времени. Здесь каждый эксперимент уникален и о массовом эксперименте речь не идет. Другое направление возникает, когда необходимо сопоставить большое число альтернатив управленческих решений. В этом случае массовый эксперимент на ЭВМ необходим. Поэтому наряду с моделями высокой организации необходимы относительно простые модели, которые обеспечивают диалог исследователя и ЭВМ и помогают сузить множество анализируемых альтернатив. Таким образом, создание математических моделей является важным этапом познания действительности. Накапливаясь, модели «раскрывают» единство материального мира в части существования в нем количественных отношений и пространственных форм. Выявляемый при этом структурный изоморфизм моделей раскрывает общность законов развития явлений природы, кажущихся иногда несравнимыми. Примером могут служить световые и электромагнитные явления, теплота и атомно-молекулярное движение и т.д.
Вопросы и упражнения 1. Что такое математическая модель? 2. Каким образом строится математическая модель объекта, процесса или явления? 3. Можно ли считать формулы, используемые в физике (химии) математическими моделями физических (химических) явлений? 4. Составить математическую модель, которая отражает зависимость толщины снежного покрова от времени выпадения осадков (снега) 5. Постройте какую-либо математическую модель вашей комнаты, например, с целью вычисления объема комнаты или определения того, какой процент площади пола свободен от мебели
Поиск по сайту: |
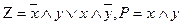 может служить математической моделью одноразрядного сумматора.
может служить математической моделью одноразрядного сумматора.