 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Собственные значения и собственные векторы матрицы
Будем рассматривать квадратные матрицы размером п х п, или, что то же самое, матрицы порядка п. При умножении матрицы порядка п на n-мерный вектор в произведении получается n-мерный вектор:
Для любой матрицы может существовать набор особых векторов, таких, что произведение матрицы на вектор из такого набора равносильно умножению этого вектора на определенное вещественное число (вообще говоря разное для каждого вектора). Определение 4. Число λ называется собственным значением матрицы А порядка п, если существует такой ненулевой вектор
При этом вектор Иными словами, умножение матрицы на ее собственный вектор равносильно удлинению этого вектора в |λ| раз, если |λ| > 1 (или сжатию при |λ| < 1). Если λ = 1, умножение матрицы на соответствующий собственный вектор не меняет его. Уравнение (13.5) представлено в матричной форме. Группируя все слагаемые этого уравнения в левой части, перепишем его в более удобном виде:
где Е и Если aij — элементы матрицы А, то характеристическая матрица А — λЕ, согласно определениям умножения матрицы на число и суммы матриц, имеет вид
Проблема отыскания собственных значений и собственных векторов матриц составляет основу специального раздела алгебры; в дальнейшем мы еще вернемся к этому вопросу. Здесь лишь отметим один важный результат алгебры матриц: для симметрических матриц (13.2) все п собственных значений являются действительными числами. Обратная матрица Ранг матрицы
Выше уже говорилось, что матрицы размера т х п можно рассматривать как системы, состоящие из m n-мерных векторов (или из п m-мерных векторов). Поскольку любая система векторов характеризуется рангом (п. 12.2), то естественно встает вопрос о такой же характеристике и для матриц. Так как здесь имеют место две совокупности векторов — векторы-строки и векторы-столбцы, то у матрицы, вообще говоря, два ранга — строчный и столбцовый. Ответ на вопрос об их равноправии дает следующая теорема. ТЕОРЕМА 1. Строчный и столбцовый ранги любой матрицы равны. Доказательство этой теоремы мы опускаем.
Стало быть, ранг любой матрицы размера т х п можно искать как ранг одной из двух систем векторов: либо т векторов-строк, либо п векторов-столбцов. Как следует из п. 12.2, для прямоугольной матрицы максимальный ранг r = min (m, n). Для квадратной матрицы размером п х n ее максимальный ранг не может превышать п: r ≤ п.
Поиск по сайту: |

 Rn, что выполняется равенство
Rn, что выполняется равенство
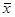 называется собственным вектором матрицы А, а λ — собственным значением матрицы А, соответствующим вектору
называется собственным вектором матрицы А, а λ — собственным значением матрицы А, соответствующим вектору 
 — соответственно единичная матрица и нулевой вектор.
— соответственно единичная матрица и нулевой вектор.