|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами)
Рассмотрим модель рынка с прогнозируемыми ценами. В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Однако спрос и предложение в реальных ситуациях зависят еще и от тенденции ценообразования и темпов изменения цены. В моделях с непрерывными и дифференцируемыми по времени t функциями эти характеристики описываются соответственно первой и второй производными функции цены P(t). Рассмотрим конкретный пример. Пусть функции спроса D и предложения S имеют следующие зависимости от цены Р и ее производных:
Принятые в (11.20) зависимости вполне реалистичны: поясним это на слагаемых с производными функции цены. 1. Спрос "подогревается" темпом изменения цены: если темп растет (Р" > 0), то рынок увеличивает интерес к товару, и наоборот. Быстрый рост цены отпугивает покупателя, поэтому слагаемое с первой производной функции цены входит со знаком минус. 2. Предложение в еще большей мере усиливается темпом изменения цены, поэтому коэффициент при Р" в функции S(t) больше, чем в D(t). Рост цены также увеличивает предложение, потому слагаемое, содержащее Р', входит в выражение для S(t) со знаком плюс. Требуется установить зависимость цены от времени. Поскольку равновесное состояние рынка характеризуется равенством D = S, приравняем правые части уравнений (11.20). После приведения подобных получаем
Соотношение (11.21) представляет линейное неоднородное дифференциальное уравнение второго порядка относительно функции P(t). Как было установлено в п. 10.3, общее решение такого уравнения состоит из суммы какого-либо его частного решения и общего решения соответствующего однородного уравнения
Характеристическое уравнение имеет вид
Его корни — комплексно-сопряженные числа: k1,2 = -1 ± 2i, и, следовательно, общее решение уравнения (11.22) дается формулой
где С1 и С2 — произвольные постоянные. В качестве частного решения неоднородного уравнения (11.21) возьмем решение Р = Pst — постоянную величину как установившуюся цену. Подстановка в уравнение (11.21) дает значение Pst:
Таким образом, общее решение уравнения (11.21) имеет вид
Нетрудно видеть, что P(t) Приведем частные решения этой задачи в двух вариантах: задача Коши и смешанная задача. 1. Задача Коши. Пусть в начальный момент времени известна цена, а также тенденция ее изменения:
Подставляя первое условие в формулу (11.23), получаем Р(0) = С1 + 3 = 4, откуда С1 = 1, т.е. имеем
Дифференцируя, имеем отсюда
Теперь реализуем второе условие задачи Коши: Р'(0) = 2C2 — 1=1, откуда C2 = 1. Окончательно получаем, что решение задачи Коши имеет вид
или в более удобной форме:
Рис.11.5
2. Смешанная задача. Пусть в начальный момент времени известны цена и спрос:
Поскольку первое начальное условие такое же, как и в предыдущем случае, то имеем и здесь решение (11.24). Тогда производные функции Р(t) выражаются формулами
Отсюда Р'(0) =2C2 - 1и Р"(0) = -4C2 - 3. Подставляя эти равенства во второе условие задачи, т.е. D(0) = 16, имеем с учетом вида D(t) из первой формулы (11.20): С2 = -1. Итак, решение данной задачи имеет вид
или в более удобной форме:
Интегральные кривые, соответствующие задачам 1 и 2, изображены на рис. 11.5.
УПРАЖНЕНИЯ 11.1. Используя формулу (11.13) динамики национального дохода Y(t) по модели Кейнса, а) проанализировать роль каждого параметра в увеличении величины Yр согласно формуле (11.12), что ведет к падению Y(t); б) вывести рекомендации по изменению параметров, описывающих основные экономические показатели; в) выбрать более предпочтительные изменения, указанные в п. б, применительно к условиям России. 11.2. Найти динамику цены Р на товар, если прогноз спроса и предложения описывается следующими соотношениями:
11.3. В условиях предыдущей задачи какой из трех случаев описывает паническое состояние на рынке и с чем это связано?
Поиск по сайту: |


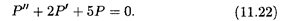


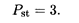

 Pst = 3 при t
Pst = 3 при t 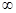 , т.е. все интегральные кривые имеют горизонтальную асимптоту Р = 3 и колеблются около нее. Это означает, что все цены стремятся к установившейся цене Pst с колебаниями около нее, причем амплитуда этих колебаний затухает со временем.
, т.е. все интегральные кривые имеют горизонтальную асимптоту Р = 3 и колеблются около нее. Это означает, что все цены стремятся к установившейся цене Pst с колебаниями около нее, причем амплитуда этих колебаний затухает со временем.