 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Фундаментальная система решений
Решения однородной системы обладают следующими свойствами. Если вектор Как мы знаем из п. 12.2, всякая система n-мерных векторов, состоящая более чем из п векторов, является линейно зависимой. Таким образом, из множества векторов-решений однородной системы (15.14) можно выбрать базис, т.е. любой вектор-решение данной системы будет линейной комбинацией векторов этого базиса. Любой такой базис называется фундаментальной системой решений однородной системы линейных уравнений. Справедлива следующая теорема, которую мы приводим без доказательства.
Укажем теперь способ нахождения фундаментальной системы решений (ФСР). Пусть система однородных уравнений (15.14) имеет ранг r < п. Тогда, как следует из правил Крамера, базисные неизвестные этой системы x1, x2, … xr линейно выражаются через свободные переменные xr+1, xr+2 , ..., xп:
Выделим частные решения однородной системы (15.14) по следующему принципу. Для нахождения первого вектора-решения
ФСР (15.16) является одним из фундаментальных наборов решений однородной системы (15.14). Пример 1. Найти решение и ФСР системы однородных уравнений
Решение. Будем решать эту систему методом Гаусса. Поскольку число уравнений системы меньше числа неизвестных, считаем х1, x2, х3 базисными неизвестными, а x4, х5, x6 — свободными переменными. Составим расширенную матрицу системы и выполним действия, составляющие прямой ход метода:
Преобразованная расширенная матрица соответствует системе уравнений, которая эквивалентна исходной однородной системе:
Обратный ход метода Гаусса дает значения базисных неизвестных, выраженные через свободные переменные:
Поскольку ранг однородной системы равен трем, то ФСР для нее состоит из трех линейно независимых векторов. По формулам (15.16) при п = 6 и r = 3, беря последовательно для свободных переменных тройки чисел (1, 0, 0), (0, 1, 0) и (0, 0, 1), получаем набор фундаментальных решений:
Поиск по сайту: |
 = (α1, α2,... ,αn) является решением системы (15.14), то и для любого числа k вектор k
= (α1, α2,... ,αn) является решением системы (15.14), то и для любого числа k вектор k  = (γ1, γ2, ... ,γn), то сумма
= (γ1, γ2, ... ,γn), то сумма  ТЕОРЕМА 4. Если ранг r системы однородных уравнений (15.14) меньше числа неизвестных п, то всякая фундаментальная система решений системы (15.14) состоит из п - r решений.
ТЕОРЕМА 4. Если ранг r системы однородных уравнений (15.14) меньше числа неизвестных п, то всякая фундаментальная система решений системы (15.14) состоит из п - r решений.
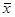 1 положим xr+1 = 1, xr+2 = xr+3 = ... = xn = 0. Затем находим второе решение
1 положим xr+1 = 1, xr+2 = xr+3 = ... = xn = 0. Затем находим второе решение 




