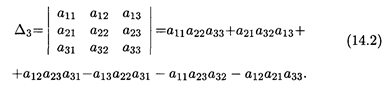Понятие обратной матрицы

Понятие обратной матрицы распространяется только на квадратные матрицы, поэтому здесь и далее мы будем иметь дело с матрицами порядка п.

Определение 1. Матрица порядка п называется вырожден­ной, если ее ранг r < п.

Определение 2. Матрица А^-1 называется обратной по отно­шению к матрице А, если их произведение равно единичной матрице:

Несколько забегая вперед, отметим, что для вырожденной матрицы не существует обратной матрицы. Иными словами, если для некоторой матрицы порядка п ее ранг r < п, то для нее не существует обратной матрицы.

УПРАЖНЕНИЯ

13.1. Найти матрицу С = 2А - В, где

13.2. Даны следующие матрицы:

Найти: а) все произведения матриц, которые имеют смысл; б) соответствующие транспонированные матрицы; в) матрицу 2G – С²,г) матрицу С³.

13.3. Дана матрица . Проверить непосредствен­ным вычислением, какие из данных ниже векторов являют­ся собственными векторами этой матрицы, и указать соответ­ствующие собственные значения:

Глава 14. ОПРЕДЕЛИТЕЛИ

Операции над определителями и основные свойства

Понятие определителя

Любой квадратной матрице А порядка n ставится в соот­ветствие по определенному закону некоторое число, называе­мое определителем, или детерминантом, n-го порядка этой матрицы. Начнем с определителей второго и третьего поряд­ков.

Пусть дана матрица

тогда ее определитель второго порядка вычисляется по фор­муле

Правило вычисления определителя второго порядка очевидно: из произведения элементов на главной диагонали вычитает­ся произведение элементов на второй диагонали матрицы А. Нетрудно видеть, что формула (14.1) представляет собой ал­гебраическую сумму двух попарных произведений элементов матрицы А, стоящих в разных строках и разных столбцах.

В дальнейшем мы не будем приводить матрицу, для кото­рой вычисляется определитель, так как в записи определителя содержатся все элементы соответствующей матрицы.

Определитель третьего порядка вычисляется по формуле

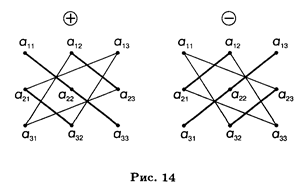
Правило вычисления определителя третьего порядка следу­ющее. Это алгебраическая сумма шести тройных произведе­ний элементов, стоящих в разных строках и разных столб­цах; со знаком плюс берутся произведения, сомножители кото­рых находятся на главной диагонали и в вершинах треугольников, чьи основания параллельны главной диагонали; со зна­ком минус — произведения, сомножители которых стоят на не главной диагонали и в вершинах треугольников с основани­ями, параллельными этой диагонали (рис. 14). Заметим, что каждое слагаемое в формуле (14.2) содержит по одному эле­менту из каждой строки и каждого столбца соответствующей матрицы.

Рассмотрим определитель n-го порядка

Теперь с учетом подмеченных выше закономерностей перейдем к определению для общего случая.

Определение 1. Определителем матрицы А n-го порядка на­зывается алгебраическая сумма n! произведений n-го порядка элементов этой матрицы, причем в каждое произведение вхо­дит по одному элементу из каждой строки и каждого столбца данной матрицы.

Поиск по сайту: