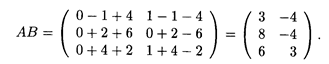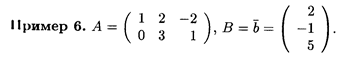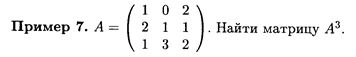|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Линейные операции над матрицами
1. Сумма матриц. Суммой матриц А и В одинакового размера называется матрица С того же размера, каждый элемент которой равен сумме соответствующих элементов матриц А и В. Представим это в сокращенной записи. Пусть
Тогда сумма этих матриц С = А + В имеет вид
Пример 1. Пусть даны матрицы А и В:
Тогда их суммой, согласно определению, является матрица
2. Умножение матрицы на действительное число. Произведением матрицы А на действительное число α называется матрица, каждый элемент которой получен умножением соответствующего элемента матрицы А на число α. Пример 2. Пусть даны матрица А и число α:
Тогда произведением матрицы А на число является матрица
3. Приведем свойства операций суммирования матриц и произведения матрицы на число, непосредственно вытекающие из определения этих операций. Пусть А, В и С — матрицы, имеющие одинаковый размер, а α и β — некоторые действительные числа. Тогда: 1) А + В = В + А, 2) (А + В) + С = А + (В + С), 3) α(А + В) =αА + αВ, 4) (α + β) A = αA + βA, 5) (αβ)А = (αA)β, 6) A + О = А, где О — нулевая матрица, 7) 0А = О.
Транспонирование матриц Транспонированием матрицы называется замена строк матрицы на ее столбцы с сохранением их порядка (или, что то же самое, замена столбцов матрицы на ее строки). Пусть дана исходная матрица А:
Тогда, согласно определению, транспонированная матрица А' имеет вид
Сокращенная форма записи операции транспонирования матрицы:
Пример 3. Пусть даны матрицы А и В:
Тогда соответствующие транспонированные матрицы имеют вид
Нетрудно заметить две закономерности операции транспонирования матриц. 1. Дважды транспонированная матрица равна исходной матрице:
2. При транспонировании квадратных матриц элементы, находящиеся на главной диагонали, не меняют своих позиций, т.е. главная диагональ квадратной матрицы не меняется при транспонировании. Важную роль в алгебре и ее приложениях играют симметрические матрицы — квадратные матрицы, у которых элементы, симметричные относительно главной диагонали, равны, т.е. aij = aji. Транспонирование таких матриц не меняет их вида, так что равенство
также можно полагать определением симметрической матрицы.
Умножение матриц 1. Умножение матриц — это специфическая операция, составляющая основу алгебры матриц. Строки и столбцы матриц можно рассматривать как векторы-строки и векторы-столбцы соответствующих размерностей: иными словами, любую матрицу можно интерпретировать как совокупность векторов-строк или векторов-столбцов. Пусть даны матрица А размером т х п и матрица В размером п х k. Будем рассматривать матрицу А как совокупность т векторов-строк
Векторы-строки матрицы А и векторы-столбцы матрицы В показаны в записи этих матриц (13.3). Длина строки матрицы А равна высоте столбца матрицы В, и потому скалярное произведение этих векторов имеет смысл.
Определение 3. Произведением матриц А и В называется матрица С, элементы которой cij равны скалярным произведениям векторов-строк
Произведение матриц А и В — матрица С — имеет размер т х k, поскольку длина п векторов-строк и векторов-столбцов исчезает при суммировании произведений координат этих векторов в их скалярных произведениях, как показано в формулах (13.4). Таким образом, для вычисления элементов первой строки матрицы С необходимо последовательно получить скалярные произведения первой строки матрицы А на все столбцы матрицы В; вторая строка матрицы С получается как скалярные произведения второй вектор-строки матрицы А на все векторы-столбцы матрицы В и так далее. Для удобства запоминания размера произведения матриц нужно перемножить отношения размеров матриц-сомножителей: В операции умножения матриц есть характерная особенность: произведение матриц А и В имеет смысл, если число столбцов в А равно числу строк в В. Тогда если А и В — прямоугольные матрицы, то произведение В и А уже не будет иметь смысла, так как в скалярных произведениях, формирующих элементы соответствующей матрицы, должны участвовать векторы с одинаковым числом координат. Если матрицы А и В квадратные размером n х n, то имеет смысл как произведение матриц АВ, так и произведение матриц BA, причем размер этих матриц такой же, как и у исходных сомножителей. При этом в общем случае перемножения матриц правило перестановочности не соблюдается, т.е. АВ ≠ ВА. Рассмотрим примеры на умножение матриц.
Решение. Поскольку число столбцов матрицы А равно числу строк матрицы В, то произведение матриц АВ имеет смысл. По формулам (13.4) получаем в произведении матрицу размером 3 х 2:
Произведение ВА не имеет смысла, так как число столбцов матрицы В не совпадает с числом строк матрицы А.
Решение. Здесь мы найдем произведения данных матриц АВ и ВА:
Как видно из результата, матрица произведения зависит от порядка расположения матриц в произведении. В обоих случаях произведения матриц имеют тот же размер, что и у исходных сомножителей: 2 х 2.
Решение. В данном случае матрица В представляет собой вектор-столбец, т.е. матрицу, у которой три строки и один столбец. Вообще, векторы — это частные случаи матриц: вектор-строка длины п представляет собой матрицу с одной строкой и п столбцами, а вектор-столбец высоты n — матрицу с n строками и одним столбцом. Размеры данных матриц соответственно 2 х 3 и 3 х 1, так что произведение этих матриц определено. Имеем
В произведении получена матрица размером 2 х 1 или вектор-столбец высоты 2.
Решение. Путем последовательного умножения матриц находим
2. Свойства произведения матриц. Пусть А, В и С — матрицы соответствующих размеров (чтобы произведения матриц были определены), а α — действительное число. Тогда следующие свойства произведения матриц имеют место: 1) (АВ)С = А(ВС), 2) (А + В)С = AC + ВС, 3) А(В + С) = АВ + АС, 4) α(АВ) = (αА)В = А(αВ). В п. 1 этого раздела введено понятие единичной матрицы Е. Нетрудно убедиться, что в алгебре матриц она играет роль единицы, т.е. можно отметить еще два свойства, связанные с умножением на эту матрицу слева и справа в случае квадратных матриц: 5) АЕ = А, 6) ЕА = А. Иными словами, произведение любой матрицы на единичную матрицу, если оно имеет смысл, не меняет исходную матрицу.
Поиск по сайту: |













 i размерности п каждый, а матрицу В — как совокупность k векторов-столбцов
i размерности п каждый, а матрицу В — как совокупность k векторов-столбцов  j, каждый из которых содержит по п координат:
j, каждый из которых содержит по п координат:
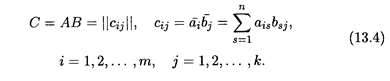
 , т.е. размер матрицы С равен произведению оставшихся в отношении чисел: т х k.
, т.е. размер матрицы С равен произведению оставшихся в отношении чисел: т х k.