 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Модель естественного роста выпуска
Будем полагать, что некоторая продукция продается по фиксированной цене Р. Обозначим через Q(t) количество продукции, реализованной на момент времени t; тогда на этот момент времени получен доход, равный PQ(t). Пусть часть указанного дохода расходуется на инвестиции в производство реализуемой продукции, т.е.
где m — норма инвестиции — постоянное число, причем 0 < т < 1. Если исходить из предположения о ненасыщаемости рынка (или о полной реализации производимой продукции), то в результате расширения производства будет получен прирост дохода, часть которого опять будет использована для расширения выпуска продукции. Это приведет к росту скорости выпуска (акселерации), причем скорость выпуска пропорциональна увеличению инвестиций, т.е.
где 1/l — норма акселерации. Подставив в (11.2) формулу (11.1), получим
Дифференциальное уравнение (11.3) представляет собой уравнение первого порядка с разделяющимися переменными. Общее решение этого уравнения имеет вид
где С — произвольная постоянная. Пусть в начальный момент времени t = t0 зафиксирован (задан) объем выпуска продукции Q0. Тогда из этого условия можно выразить постоянную С: Q0 = С
Заметим, что математические модели обладают свойством общности. Так, из результатов биологических опытов следует, что процесс размножения бактерий также описывается уравнением (11.3). Процесс радиоактивного распада подчиняется закономерности, установленной формулой (11.4).
Рост выпуска в условиях конкуренции
В этой модели мы снимем предположение о ненасыщаемости рынка. Пусть Р = Р(Q) — убывающая функция, т.е. с увеличением объема продукции на рынке цена на нее падает: dP/dQ < 0. Теперь из формул (11.1)-(11.3) мы получаем нелинейное дифференциальное уравнение первого порядка относительно Q с разделяющимися переменными:
Поскольку все сомножители в правой части этого уравнения положительны, то Q' > 0, т.е. функция Q(t) возрастающая. Характер возрастания функции определяется ее второй производной. Из уравнения (11.5) получаем
Это равенство можно преобразовать, введя эластичность спроса
или, так как
Из уравнения (11.6) следует, что Q" > 0 при эластичном спросе, т.е. когда |Е| > 1, и график функции Q(t) имеет направление выпуклости вниз, что означает прогрессирующий рост. При неэластичном спросе |Е| < 1, и в этом случае Q" < 0 — направление выпуклости функции Q(t) вверх, что означает замедленный рост (насыщение). Для простоты примем зависимость P(Q) в виде линейной функции
(рис. 11.1). Тогда уравнение (11.5) имеет вид
откуда
Из соотношений (11.7) и (11.8) получаем: Q' = 0 при Q = 0 и при Q = а/b, Q" > 0 при Q < а /(2b) и Q" < 0 при Q > а/(2b); Q = a/(2b) — точка перегиба графика функции Q = Q(t). Приведенный на рис. 11.2 график этой функции (одной из интегральных кривых дифференциального уравнения (11.7)) носит название логистической кривой.
Аналогичные кривые характеризуют и другие процессы, например размножение бактерий в ограниченной среде обитания, динамику эпидемий внутри ограниченной общности биологических организмов и др.
Динамическая модель Кейнса
Рассмотрим простейшую балансовую модель, включающую в себя основные компоненты динамики расходной и доходной частей экономики. Пусть Y(t), E(t), S(t), I(t) — соответственно национальный доход, государственные расходы, потребление и инвестиции. Все эти величины рассматриваются как функции времени t. Тогда справедливы следующие соотношения:
где a(t) — коэффициент склонности к потреблению (0 < а(t) < 1), b(t) — автономное (конечное) потребление, k(t) — норма акселерации. Все функции, входящие в уравнения (11.9), положительны. Поясним смысл уравнений (11.9). Сумма всех расходов должна быть равной национальному доходу — этот баланс отражен в первом уравнении. Общее потребление состоит из внутреннего потребления некоторой части национального дохода в народном хозяйстве и конечного потребления — эти составляющие показаны во втором уравнении. Наконец, размер инвестиций не может быть произвольным: он определяется произведением нормы акселерации, величина которой характеризуется уровнем технологии и инфраструктуры данного государства, на предельный национальный доход. Будем полагать, что функции a(t), b(t), k(t) и E(t) заданы — они являются характеристиками функционирования и эволюции данного государства. Требуется найти динамику национального дохода, или Y как функцию времени t. Подставим выражения для S(t) из второго уравнения и для I(t) из третьего уравнения в первое уравнение. После приведения подобных получаем дифференциальное неоднородное линейное уравнение первого порядка для функции Y(t):
Согласно п. 9.4, существует достаточно сложная формула общего решения этого уравнения. Мы проанализируем более простой случай, полагая основные параметры задачи а, b и k постоянными числами. Тогда уравнение (11.10) упрощается до линейного дифференциального уравнения первого порядка с постоянными коэффициентами:
Как известно, общее решение неоднородного уравнения есть сумма какого-либо его частного решения и общего решения соответствующего однородного уравнения. В качестве частного решения уравнения (11.11) возьмем так называемое равновесное решение, когда Y’ = 0, т.е.
Нетрудно видеть, что эта величина положительна. Общее решение однородного уравнения дается формулой
Интегральные кривые уравнения (11.11) показаны на рис. 11.3. Если в начальный момент времени Y0 < Yp , то С = Y0 — Yp < 0и кривые уходят вниз от равновесного решения (11.12), т.е. национальный доход со временем падает при заданных параметрах задачи а, b, k и Е, так как показатель экспоненты в (11.13) положителен. Если же Y0 > Yp, то С > 0 и национальный доход растет во времени — интегральные кривые уходят вверх от равновесной прямой Y = Yр. Согласно классификации п. 9.3, уравнение (11.11) является автономным; точка Y = Yp представляет собой точку неустойчивого равновесия.
Неоклассическая модель роста
Пусть Y = F (K, L) — национальный доход, где F — однородная производственная функция первого порядка (F (tK, tL) = tF (K, L)), К — объем капиталовложений (производственных фондов), L — объем затрат труда. Введем в рассмотрение величину фондовооруженности k = K/L, тогда производительность труда выражается формулой
Целью задачи, рассматриваемой в этом разделе, является описание динамики фондовооруженности или представление ее как функции от времени t. Поскольку любая модель базируется на определенных предпосылках, нам нужно сделать некоторые предположения и ввести ряд определяющих параметров. В данном случае будем полагать, что выполнены следующие предположения. 1. Имеет место естественный прирост во времени трудовых ресурсов:
2. Инвестиции расходуются на увеличение производственных фондов и на амортизацию, т.е.
где β — норма амортизации. Тогда если l — норма инвестиций, то I = lY = К' + βК, или
Из определения фондовооруженности k вытекает, что
Дифференцируя это равенство по t, имеем
Подставив в это соотношение выражения (11.15) и (11.16), получаем уравнение относительно неизвестной функции k
где функция f(k) определена по формуле (11.14). Полученное соотношение (11.17) представляет собой нелинейное дифференциальное уравнение первого порядка с разделяющимися переменными (которое является автономным). Выделим стационарное решение этого уравнения; из условия k' = 0 следует, что
т.е. k = const — постоянная величина, являющаяся корнем этого нелинейного алгебраического уравнения. Рассмотрим конкретную задачу: для производственной функции F(K, L) =
Стационарное решение этого уравнения следует из равенства
откуда получаем ненулевое частное решение уравнения (11.17): kst = I2/(α + β)2.
Рис. 11.4
Дифференциальное уравнение (11.17) решаем методом разделения переменных:
Интегрируя это уравнение с заменой переменной
Семейство интегральных кривых сходится сверху и снизу к стационарному решению (рис. 11.4): т.е. k
Поиск по сайту: |




 , откуда С = Q0
, откуда С = Q0  . Отсюда получаем частное решение уравнения (11.3) — решение задачи Коши для этого уравнения:
. Отсюда получаем частное решение уравнения (11.3) — решение задачи Коши для этого уравнения:


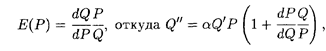
 < 0, а значит, и Е < 0, окончательно получаем
< 0, а значит, и Е < 0, окончательно получаем
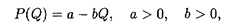

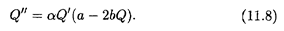






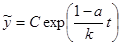 , так что общее решение уравнения (11.11) имеет вид
, так что общее решение уравнения (11.11) имеет вид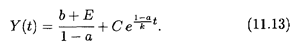









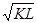 найти интегральные кривые уравнения (11.17) и стационарное решение.Из (11.14) следует, что f(k) =
найти интегральные кривые уравнения (11.17) и стационарное решение.Из (11.14) следует, что f(k) =  , и тогда уравнение (11.17) имеет вид
, и тогда уравнение (11.17) имеет вид




 kst при t
kst при t 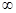 . Следовательно, при неизменных входных параметрах задачи l, α и β функция фондовооруженности в данном случае устойчиво стремится к стационарному значению независимо от начальных условий. Такая стационарная точка k = kst является точкой устойчивого равновесия.
. Следовательно, при неизменных входных параметрах задачи l, α и β функция фондовооруженности в данном случае устойчиво стремится к стационарному значению независимо от начальных условий. Такая стационарная точка k = kst является точкой устойчивого равновесия.