 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Ранг матрицы и системы векторов
1. Пусть дана матрица, содержащая m строк и п столбцов:
Выделим в ней произвольным образом k строк и k столбцов. Элементы, которые находятся на пересечении выделенных строк и столбцов, образуют квадратную матрицу k-го порядка; определитель этой матрицы называется минором k-го порядка матрицы А. Очевидно, что в общем случае таких миноров k-го порядка может быть несколько. При этом максимальный порядок миноров равен минимальному из чисел т и п, т.е.
Из всех возможных миноров матрицы А выделим те из них, которые отличны от нуля. В свою очередь среди этих миноров можно найти по крайней мере один минор наибольшего порядка. Определение 1. Наибольший порядок миноров, отличных от нуля, называется рангом матрицы (14.5). Определение 2. Отличный от нуля минор матрицы, порядок которого равен рангу матрицы, называется базисным минором этой матрицы. Столбцы и строки матрицы, участвующие в образовании базисного минора, также называются базисными.
Заметим, что в общем случае у матрицы может быть несколько базисных миноров. В п. 13.2 было дано определение ранга матрицы как наибольшего числа линейно независимых ее векторов-строк (столбцов). В курсе алгебры доказывается, что эти два определения эквивалентны. Приведенное в данном разделе определение дает возможность вычислять ранг матрицы, а значит, и ранг системы векторов. Пример 1. Найти ранг матрицы размером 4 х 6:
Решение. Нетрудно видеть, что максимальный порядок миноров этой матрицы, отличных от нуля, равен двум, поскольку миноры третьего порядка должны содержать элементы по крайней мере двух строк со второй по четвертую. Такие определители равны нулю либо по признаку пропорциональности двух строк, либо по признаку наличия в них нулевой строки. У этой матрицы существуют три базисные строки (либо 1-я и 2-я, либо 1-я и 3-я), и пять ее столбцов являются базисными (либо с 1-го по 5-й, либо со 2-го по 6-й); из них и формируются все базисные миноры второго порядка.
2. Рассмотрим квадратную матрицу порядка п, т.е. когда в матрице (14.5) т = п. Как было отмечено в п. 13.2, матрица порядка n является вырожденной и не имеет обратной матрицы, если ее ранг r < п. Максимальный порядок минора квадратной матрицы равен n; в этом случае базисный минор равен определителю этой матрицы. Стало быть, квадратная матрица является вырожденной, если ее определитель равен нулю. УПРАЖНЕНИЯ 14.1. Вычислить определители:
14.2. Дана матрица
Найти миноры элементов a23, a14, a34 и алгебраические дополнения элементов a32, a43, a24. 14.3. Найти ранги следующих матриц:
14.4. Определить, являются ли зависимыми векторы 14.5. Показать, что векторы
Поиск по сайту: |
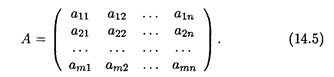





 1,
1,