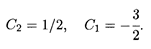Краевая задача для дифференциального уравнения второго порядка

Как было сказано в п. 10.1, в силу основной теоремы су­ществования и единственности решения для уравнения второ­го порядка

определена задача Коши, когда в точке х = x₀ заданы значения неизвестной функции и ее производной:

Если выполнены условия теоремы 10.1, то задача Коши (10.13), (10.14) однозначно определяет частное решение.

Однако существует и другой тип задач для дифференци­альных уравнений второго порядка — значения неизвестной функции задаются в двух разных точках. Иными словами, при решении уравнения (10.13) на интервале (а, b) рассмотрим гра­ничные условия наиболее простого вида на концах интервала

В этом случае уравнение (10.13) совместно с условиями (10.14) называется первой краевой задачей для уравнения второго по­рядка. Поскольку второе условие в (10.15) равносильно второ­му условию в (10.14), то указанная краевая задача может иметь единственное решение, т.е. определять единственным образом частное решение дифференциального уравнения (10.13), прохо­дящее через точки (x₁, y₁), (x₂, y₂). Так, для линейного диффе­ренциального уравнения второго порядка первая краевая зада­ча имеет решение, если определитель системы линейных алгеб­раических уравнений относительно произвольных постоянных C₁ и С₂

реализующей краевые условия (10.15), отличен от нуля. Здесь в соответствии с теоремой 10.4 (x) — частное решение не­однородного уравнения, у₁(х) и у₂(х) — линейно независимые решения соответствующего однородного уравнения. В таком случае краевая задача с условиями (10.15) однозначно опреде­ляет частное решение дифференциального уравнения (10.8).

Пример 1. Найти частное решение уравнения

удовлетворяющее краевым условиям

Общее решение этого уравнения было найдено в примере 4 и. 10.3:

Для отыскания частного решения, соответствующего данным краевым условиям, подставим это решение в эти краевые усло­вия. Получаем систему линейных уравнений относительно про­извольных постоянных С₁ и С₂

Нетрудно видеть, что определитель этой системы не равен ну­лю, т.е. данная краевая задача имеет решение. Вычитая из второго уравнения первое, умноженное на 2, получаем С₂, а затем из первого уравнения — С₁:

Отсюда решение данной краевой задачи как частное решение дифференциального уравнения, проходящее через точки (0, 1) и (ln 2, 2), имеет вид

УПРАЖНЕНИЯ

Найти общие решения линейных однородных уравнений с по­стоянными коэффициентами.

Найти общие решения неоднородных уравнений.

Найти решения уравнений второго порядка, удовлетворяющих указанным условиям задачи Коши.

Найти решения уравнений второго порядка, удовлетворяющих заданным краевым условиям.

Глава 11. АППАРАТ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЭКОНОМИКЕ

В этой главе мы рассмотрим некоторые примеры примене­ния теории дифференциальных уравнений в непрерывных мо­делях экономики, где независимой переменной является вре­мя t. Такие модели достаточно эффективны при исследовании эволюции экономических систем на длительных интервалах времени; они являются предметом исследования экономичес­кой динамики.

Поиск по сайту: