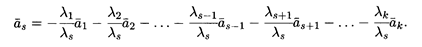Линейно зависимые и линейно независимые системы векторов

При решении различных задач, как правило, приходится иметь дело не с одним вектором, а с некоторой совокупнос­тью векторов одной размерности. Такие совокупности называ­ют системой векторов и обозначают одной буквой и порядко­вым номером:

Определение 1. Линейной комбинацией векторов (12.6) назы­вается вектор вида

где λ₁, λ₂, ..., λ_k — любые действительные числа.

Например, пусть даны три вектора: ₁ = (1, 2, 0), ₂ = (2, 1, 1) и ₃ = (-1, 1, -2). Их линейной комбинацией с коэффициентами соответственно 2, 3 и 4 является вектор = (4, 11, -5).

В случае равенства (12.7) говорят также, что вектор ли­нейно выражается через векторы (12.6) или разлагается по этим векторам.

Определение 2. Система ненулевых векторов (12.6) называ­ется линейно зависимой, если существуют такие числа λ₁, λ₂, ..., λ_k, не равные одновременно нулю, что линейная комбина­ция данной системы с указанными числами равна нулевому вектору:

Если же равенство (12.8) для данной системы векторов (12.6) возможно лишь при λ₁ = λ₂ = ... = λ_k = 0, то эта система векторов называется линейно независимой.

Например, система двух векторов ₁ = (1, 0) и ₂ = (0, 2) является линейно независимой; система двух векторов ₁ = (1, 2, 1) и ₂ = (2, 4, 2) является линейно зависимой, так как ₂ — 2 ₁ = .

Пусть система векторов (12.6) является линейно зависи­мой. Выберем в сумме (12.8) слагаемое, в котором коэффициент λ_s ≠ 0, и выразим его через остальные слагаемые:

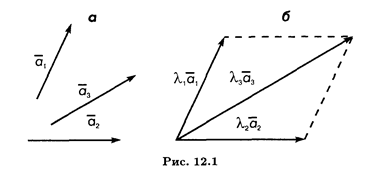
Как видно из этого равенства, один из векторов линейно зави­симой системы (12.7) оказался выраженным через другие век­торы этой системы (или разлагается по остальным ее векто­рам).

Укажем свойства линейно зависимой системы векторов.

1. Система, состоящая из одного ненулевого вектора, ли­нейно независима.

2. Система, содержащая нулевой вектор, всегда линейно за­висима.

3. Система, содержащая более одного вектора, линейно за­висима тогда и только тогда, когда среди ее векторов содер­жится по крайней мере один вектор, который линейно выра­жается через остальные.

Геометрический смысл линейной зависимости векторов очевиден для случаев двумерных векторов на плоскости и трех­мерных векторов в пространстве. В случае двух векторов, ког­да один вектор выражается через другой, мы имеем

т.е. эти векторы коллинеарны, или, что то же самое, находятся на параллельных прямых. В пространственном случае три ли­нейно зависимых вектора параллельны одной плоскости, т.е. компланарны (рис. 12.1); достаточно "подправить" соответ­ствующими сомножителями длины этих векторов, чтобы один из них стал суммой двух других или выражался через них.

Справедлива следующая теорема, которую мы приводим без доказательства.

ТЕОРЕМА 1. В пространстве Rⁿ любая система, содержа­щая т векторов, линейно зависима при т > п.

Поиск по сайту: