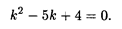|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Однородные уравнения второго порядка
Рассмотрим линейное однородное уравнение
где р и q — вещественные числа. Линейное дифференциальное уравнение второго порядка, как следует из теоремы 10.1, может иметь множество решений. Однако среди них выделяют базисные решения, по которым строится общее решение уравнения. Таких решений для уравнения второго порядка — два, каков и порядок уравнения. Определение 3. Решения у1(х) и у2(х) уравнения (10.9) называются линейно независимыми, если их линейная комбинация равна нулю:
лишь в том случае, когда С1 = C2 = 0. В том случае, когда можно найти такие числа С1 и С2, не равные нулю одновременно, что для функций у1(х) и у2(х) на некотором интервале (a, b) выполняется равенство (10.10) для любого х ТЕОРЕМА 2. Пусть решения у1(х) и у2(х) уравнения (10.9) линейно независимы на интервале (а, b). Тогда функция
где С1 и С2 — произвольные постоянные, является общим решением однородного уравнения (10.9). Эта теорема, по сути дела, выражает метод нахождения общего решения однородного дифференциального уравнения второго порядка: нужно отыскать два линейно независимых решения и взять их линейную комбинацию вида (10.11). Будем искать решение уравнения (10.9) в виде у = еkx, где k — некоторое число. Подставляя эту функцию в уравнение (10.9), получаем
Сокращая обе части этого равенства на еkx, получаем квадратное уравнение относительно k
Стало быть, если число k является корнем уравнения (10.12), то функция у = еkx есть решение однородного уравнения (10.9). Уравнение (10.10) называется характеристическим уравнением для дифференциального уравнения (10.9). Вид общего решения уравнения (10.9) существенно зависит от того, какие корни имеет характеристическое уравнение (10.10). Обозначим эти корни через k1 и k2. Справедлива следующая теорема. ТЕОРЕМА 3. А) Если корни характеристического уравнения вещественные и k1 ≠ k2, то общее решение однородного дифференциального уравнения (10.9) имеет вид
Б) если корни уравнения (10.12) вещественные и равные между собой (k1 = k2 = k), то общее решение уравнения (10.9) имеет вид
В) если корни характеристического уравнения комплексные (k1 = а + bi, k2 = а — bi, где i =
где а = -р/2, b = Заметим, что когда дискриминант характеристического уравнения (10.12) отрицательный, корни характеристического многочлена с действительными коэффициентами представляют собой комплексно-сопряженные числа; в случае В использована их алгебраическая форма. Рассмотрим примеры отыскания общих решений однородных дифференциальных уравнений второго порядка.
Решение. Характеристическое уравнение данного дифференциального уравнения имеет вид
Его корни вещественные и различны: k1 =1, k2 = 4. Следовательно, общее решение данного уравнения имеет вид
Решение. Составим характеристическое уравнение:
Оно имеет кратный корень k =3; следовательно, общее решение данного однородного уравнения имеет вид
Решение. Соответствующее характеристическое уравнение
имеет дискриминант, равный —1, и, значит, комплексно-сопряженные корни таковы: k1 = 1 + i, k2 = 1 — i, где i =
Поиск по сайту: |


 (а, b), эти функции называются линейно зависимыми на интервале (а, b). Линейная зависимость функций означает их пропорциональность, например, у1(х)/у2(х) = —С2/С1, при у2(х) ≠ 0 и С1 ≠ 0.
(а, b), эти функции называются линейно зависимыми на интервале (а, b). Линейная зависимость функций означает их пропорциональность, например, у1(х)/у2(х) = —С2/С1, при у2(х) ≠ 0 и С1 ≠ 0.
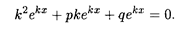



 , a и b — вещественные числа), то общее решение уравнения (10.9) имеетвид
, a и b — вещественные числа), то общее решение уравнения (10.9) имеетвид
 . Во всех трех случаях С1 и С2 — произвольные постоянные.
. Во всех трех случаях С1 и С2 — произвольные постоянные.