 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Уравнения, допускающие понижение порядка
Существуют три вида уравнения (10.2), которые при помощи замены переменной (искомой функции) сводятся к уравнениям первого порядка. 1. Уравнение вида
Введем новую функцию z(x) путем замены z(x) = у'. Тогда исходное уравнение второго порядка преобразуется в неполное уравнение первого порядка: z' = f(x), решением которого является функция z(х) =
где С1 и С2 — произвольные постоянные. 2. Уравнение вида
т.е. уравнение не содержит в явном виде у. Как и в предыдущем случае, положим z(x) = у'. Тогда получаем уравнение первого порядка общего вида z' = f(x, z). Найдя общее решение этого уравнения z = φ(x, C1), повторным интегрированием получим искомое общее решение уравнения (10.5):
где С1 и С2 — произвольные постоянные. 3. Уравнение вида
т.е. уравнение не содержит независимой переменной x. Здесь мы вводим новую функцию, зависящую от у, полагая z(y) = у'. Тогда, поскольку по правилу дифференцирования сложной функции
то уравнение (10.6) преобразуется в дифференциальное уравнение первого порядка относительно функции z(y):
Пусть общее решение этого уравнения z = φ(у, С1). Тогда обратной заменой получаем неполное уравнение первого порядка относительно функции у(х)
из которого методом разделения переменных получаем функциональное соотношение для определения общего решения уравнения (10.6):
где С1 и C2 — произвольные постоянные. Рассмотрим два примера решения дифференциальных уравнений второго порядка.
Решение. Это уравнение вида (10.5), поскольку оно не содержит в явном виде у. Заменой z(x) = у' приведем его к уравнению первого порядка
где С1 и С2 — произвольные постоянные. В зависимости от выбора знака С1 интеграл в правой части этого равенства (обозначим его через I) может иметь разные выражения:
Решение. Это уравнение вида (10.6), т.е. оно не содержит явно независимой переменной х. Заменой z(y) = у' сведем его к уравнению первого порядка
Первое решение этого уравнения z = 0, или у = С, где С — постоянная величина. Сокращая после этого обе части уравнения на z, получаем
Разделение переменных x и у приводит к общему решению исходного уравнения: e-ydy = C1dx, откуда e-y = С1х + С2, или окончательно
где С1 и С2 — произвольные постоянные. Нетрудно видеть, что это решение включает в себя и решение у = С, указанное выше (при С1 = 0, С2 ≠ 0). Далее мы рассмотрим наиболее употребимый в математических приложениях вид дифференциальных уравнений второго порядка.
Поиск по сайту: |

 f(x) dx + С1. Поскольку z(x) = у', то повторным интегрированием находим общее решение уравнения (10.4):
f(x) dx + С1. Поскольку z(x) = у', то повторным интегрированием находим общее решение уравнения (10.4):








 = -xz2, откуда имеем z =
= -xz2, откуда имеем z =  , или у' =
, или у' = 
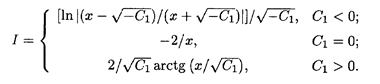


 — z = 0. Решение этого уравнения методом разделения переменных у и z дает z = С1ey. Наконец, обратная замена приводит к уравнению первого порядка
— z = 0. Решение этого уравнения методом разделения переменных у и z дает z = С1ey. Наконец, обратная замена приводит к уравнению первого порядка
