 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Применение в экономике. Предельные показатели в микроэкономике
Предельные показатели в микроэкономике
Приведем примеры двух предельных показателей в микроэкономике. 1. Первый из них связан с зависимостью себестоимости С произведенной продукции от ее объема Q: С = f(Q). Так называемая предельная себестоимость характеризует себестоимость ΔC прироста продукции ΔQ:
В предположении о непрерывной зависимости ΔС от ΔQ естественно напрашивается замена разностного отношения в (5.13) его пределом:
Обычно в приложениях с использованием аппарата математики под предельной себестоимостью понимают именно величину (5.13а). Например, пусть зависимость издержек производства от объема выпускаемой продукции выражается формулой
Определим средние и предельные издержки при объеме продукции Q = 15 ден. ед. А) Функция средних издержек на единицу продукции определяется по формуле
откуда Б) Предельные издержки определяются, согласно (5.13а), по формуле
откуда при Q = 15 получаем С' (15) = 19,75 ден. ед. Иными словами, при средних издержках на производство единицы продукции в 33,25 ден. ед. дополнительные затраты на производство единицы дополнительной продукции составят 19,75 ден. ед. и не превысят средних издержек. 2. В анализе и прогнозах ценовой политики применяется понятие эластичности спроса. Пусть D = f(Р) — функция спроса от цены товара Р (см. п. 3.1). Тогда под эластичностью спроса понимается процентное изменение спроса при изменении цены товара на один процент:
Как и в предыдущем случае, в случае непрерывной зависимости ΔD от ΔQ удобно перейти к пределу при ΔР
Аналогичное понятие можно ввести и для функции предложения S(P). Напомним, что функция D(P) убывает, а функция S(P) возрастает с ростом цены Р. Укажем некоторые свойства эластичности. Как следует из формулы (5.14а), ее можно выразить так:
Из равенства (5.14 б) следует, что E(D) обладает свойствами логарифма, а значит,
Заметим, что поскольку функция D(P) убывающая, то D'(P) < 0, а тогда согласно формуле (5.14а) и E(D) < 0. Напротив, поскольку функция предложения возрастающая, то соответствующая эластичность E(S) > 0. Различают три вида спроса в зависимости от величины |E(D)|: а) если |E(D)| > 1 (E(D) < -1), то спрос считается эластичным; б) если |E(D)| = 1 (E(D) = -1), то спрос нейтрален; в) если |E(D)| < 1 (E(D) > -1), то спрос неэластичный. Рассмотрим два примера из этой области. Пример 1. Пусть функция спроса описывается формулой
где D0 и k — известные величины. Найти, при каких значениях цены Р спрос будет эластичным. Решение. Согласно формуле (5.14а) составляем выражение для E(D):
Для того чтобы спрос был эластичным (случай а), необходимо, чтобы выполнялось неравенство
Пример 2. Найти изменение выручки с увеличением цены на товар при разных вариантах эластичности спроса. Решение. Выручка I равна произведению цены Р на товар на величину спроса D:
Найдем производную этой функции:
Теперь проанализируем все варианты эластичности спроса, приведенные выше, с учетом формулы (5.14а). 1) E(D) < -1; тогда, подставляя (5.14а) в это неравенство, получаем, что правая часть уравнения (5.15) отрицательна. Таким образом, при эластичном спросе повышение цены Р ведет к снижению выручки. Напротив, снижение цены на товар увеличивает выручку. 2) E(D) = -1. Из (5.14а) следует, что правая часть (5.15) равна нулю, т.е. при нейтральном спросе изменение цены на товар не влияет на выручку. 3) E(D) > -1. Тогда I'(P) > 0, т.е. при неэластичном спросе повышение цены Р на товар приводит к росту выручки. Понятие эластичности распространяется и на другие области экономики. Рассмотрим один характерный пример. Пример 3. Пусть зависимость между себестоимостью продукции С и объемом Q ее производства выражается формулой
Требуется определить эластичность себестоимости при выпуске продукции Q = 30 ден. ед. Решение. По формуле (5.14а) получаем
откуда при Q = 30 искомая эластичность составит около —0,32, т.е. при данном объеме выпуска продукции его увеличение на 1% приведет к снижению себестоимости примерно на 0,32%.
Максимизация прибыли
Пусть Q — количество реализованного товара, R(Q) — функция дохода; C(Q) — функция затрат на производство товара. В реальности вид этих функций зависит в первую очередь от способа производства, организации инфраструктуры и т.п. Прибыль от реализации произведенного товара дается формулой
В микроэкономике известно утверждение: для того чтобы прибыль была максимальной, необходимо, чтобы предельный доход и предельные издержки были равны. Оба упомянутых предельных показателя определяются по аналогии с (5.14а), так что этот принцип можно записать в виде R'(Q) = C'(Q). Действительно, из необходимого условия экстремума для функции (5.16) следует, что П'(Q) = 0, откуда и получается основной принцип. Пример 4. Найти максимум прибыли, если доход и издержки определяются следующими формулами:
Решение. Согласно (5.16), прибыль П(Q) = - Q3 + 36Q2 - 69Q — 4000. Приравнивая производную функции прибыли к нулю, получаем уравнение
Корни этого уравнения Q1 = 1, Q2 = 23. Проверка показывает, что максимальная прибыль достигается при Q = 23: Пmах = 1290.
Закон убывающей эффективности производства
Этот закон утверждает, что при увеличении одного из основных факторов производства, например капитальных затрат К, прирост производства начиная с некоторого значения К является убывающей функцией. Иными словами, объем произведенной продукции V как функция от К описывается графиком со сменой выпуклости вниз на выпуклость вверх. Пример 5. Пусть эта функция дается уравнением
где b и с — известные положительные числа (они определяются прежде всего структурой организации производства), а Vlim — предельно возможный объем выпускаемой продукции. Нетрудно подсчитать, что вторая производная функции (5.17) имеет вид
Критическая точка находится из условия V"(K) = 0, откуда
График функции (5.17) приведен на рис. 5.10. В точке перегиба (5.18) выпуклость графика функции вниз меняется на выпуклость вверх. До этой точки увеличение капитальных затрат приводит к интенсивному росту объема продукции: темп прироста объема продукции (аналог первой производной) возрастает, т.е. V"(K) > 0. При К > Кcr темп прироста объема выпускаемой продукции снижается, т.е. V"(K) < 0, и эффективность увеличения капитальных затрат падает.
Таким образом, в стратегии капиталовложений оказывается очень важным моментом определение критического объема затрат, сверх которого дополнительные затраты будут приводить все к меньшей отдаче при данной структуре организации производства. Зная этот прогноз, можно пытаться совершенствовать и менять структуру организации производства: "улучшать" показатели b, с и Vlim в сторону повышения эффективности капиталовложений.
УПРАЖНЕНИЯ
Найти пределы с использованием правила Лопиталя. 5.1. 5.3. 5.5. 5.8. 5.10. 5.12. Разложить по формуле Маклорена функцию f(x) = tg x до члена с x3 включительно. 5.13. Разложить по формуле Маклорена функцию f(x) = e-x до члена с x2 включительно.
Найти пределы с использованием разложений по формуле Маклорена. 5.14. 5.16.
Найти интервалы выпуклости и точки перегиба графиков функций. 5.18. 5.20.
Найти асимптоты графиков функций. 5.21. 5.23.
Исследовать и построить графики функций. 5.24. 5.26. 5.28. 5.30. 5.32.
Решите задачи на наибольшее и наименьшее значения. 5.34. Разложить число 12 на два слагаемых так, чтобы их произведение было наибольшим. 5.35. Определить размеры открытого бассейна с квадратным дном объемом V, при которых на облицовку дна и стен пойдет наименьшее количество материала. 5.36. Даны точки А(0, 3) и В(4, 5). На оси Ох найти точку, сумма расстояний от которой до точек А и В наименьшая.
Решите задачи с экономическим содержанием. 5.37. Зависимость между издержками производства С и объемом продукции Q выражается функцией С = 30Q — 0,08Q3. Определить средние и предельные издержки при объеме продукции: а) Q = 5 ед., б) Q = 10 ед. 5.38. Функции долговременного спроса D и предложения S от цены р на мировом рынке нефти имеют соответственно вид
1) Найти эластичность спроса в точке равновесной цены. 2) Как изменятся равновесная цена и эластичность спроса при уменьшении предложения нефти на рынке на 25%? 5.39. Функции спроса D и предложения S от цены р выражаются соответственно уравнениями
Найти эластичность спроса и предложения при равновесной цене, а также изменение дохода (в процентах) при увеличении цены на 10%. 5.40. Зависимость объема выпуска продукции V от капитальных затрат К определяется функцией V = V0 ln (4 + K3). Найти интервал изменения К, на котором увеличение капитальных затрат неэффективно.
Поиск по сайту: |



 = C/Q, или в нашем случае
= C/Q, или в нашем случае


 0:
0:


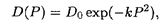
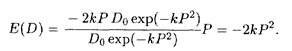









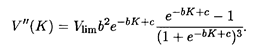


 .5.2.
.5.2.  .
. .5.4.
.5.4.  .
. .5.6.
.5.6.  .5.7.
.5.7.  .
. .5.9.
.5.9. 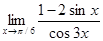 .
.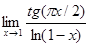 .5.11.
.5.11. 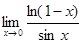 .
. . 5.15.
. 5.15. 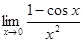 .
. .5.17.
.5.17.  .
. .5.19.
.5.19. 
 .
. . 5.22.
. 5.22.  .
. .
. .5.25.
.5.25.  .
. . 5.27.
. 5.27.  .
. .
. . 5.31.
. 5.31. 
 .5.33.
.5.33.  .
.
