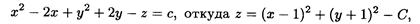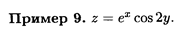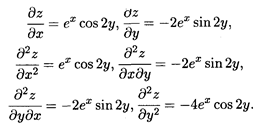|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Частные производные функции нескольких переменных
Частные производные первого порядка
Пусть функция двух переменных z = f(x, у) определена в некоторой окрестности точки М(x, у) евклидова пространства Е2. Частная производная функции z = f(x, у) по аргументу x является обыкновенной производной функции одной переменной х при фиксированном значении переменной у и обозначается как
Аналогичным образом определяется частная производная функции f(x, у) по переменной у в точке М, обозначаемая как
Функция, имеющая частные производные, называется дифференцируемой. Совершенно аналогично определяются частные производные функций трех и более переменных. Частная производная функции нескольких переменных характеризует скорость ее изменения по данной координате при фиксированных значениях других координат. Найти частные производные следующих функций.
Решение. Дифференцируем функцию z = f(x, y) сначала по х, полагая у фиксированной величиной, потом повторяем эту же процедуру, меняя роли x и у. Получаем
Ррешение. Частные производные этой функции трех переменных выражаются следующими формулами:
Пример 4. Найти предельные показатели продукции Q при изменении одного из факторов: затрат капитала К или величины трудовых ресурсов L — по функции Кобба—Дугласа
Решение. Частные производные этой функции
дают решение сформулированной выше задачи. Очевидно, что в функции Кобба—Дугласа показатели степеней α и l — α представляют собой соответственно коэффициенты эластичности EK(Q) и EL(Q) по каждому из входящих в нее аргументов.
Градиент
Рассмотрим функцию трех переменных и = f(x, у, z), дифференцируемую в некоторой точке M(x, y, z). Определение 1. Градиентом функции и = f(x, у, z) называется вектор, координаты которого равны соответственно частным производным Для обозначения градиента функции используется символ
Аналогично в случае функции двух переменных и = f(x, у) имеем
Градиент функции характеризует направление и величину максимальной скорости возрастания этой функции в точке. Для определения геометрического смысла градиента функции введем понятие поверхности уровня. Это понятие аналогично понятию линии уровня, рассмотренному в п. 8.2. Определение 2. Поверхностью уровня функции и = f(x, у, z) называется поверхность, на которой эта функция сохраняет постоянное значение
В курсе математического анализа доказывается, что градиент в данной точке ортогонален к этой поверхности. В случае функции двух переменных все сказанное выше остается в силе, только вместо поверхности уровня будет фигурировать линия уровня. Рассмотрим некоторые примеры. Пример 5. Найти градиент и его модуль функции z = Решение. По формуле (8.8) имеем для функции двух переменных
При х = 0 и у = 1 получаем
Пример 6. Найти градиент и его модуль функции и = x2 + у2 - z2 в точке М (1, 1, -2). Решение. По формуле (8.7) имеем
Подставляя в это выражение координаты точки М, получаем
Пример 7. Найти поверхности уровня функции u = х2 — 2х + у2 + 2у — z. Решение. Согласно определению поверхности уровня (8.9) имеем
где С = с + 2. Следовательно, поверхностями уровня данной функции являются параболоиды вращения с осью х = 1, у = -1, параллельной оси Oz, вершины которых лежат в точках с координатами (1, -1, -С).
Частные производные высших порядков
Частные производные первого порядка от функции двух и более переменных также представляют собой функции нескольких переменных, и их можно также продифференцировать, т.е. найти частные производные от этих функций. Так, для функции двух переменных вида z = f(x, у) возможны четыре вида частных производных второго порядка:
Частные производные, в которых дифференцирование производится по разным переменным, называются смешанными производными. Аналогичным образом для функций нескольких переменных определяются частные производные более высоких порядков. Рассмотрим два примера нахождения частных производных второго порядка для функции двух переменных.
Решение. Последовательно дифференцируя, получаем
Решение. По правилам дифференцирования произведения имеем
В рассмотренных примерах смешанные производные оказались равными друг другу, хотя это бывает и не всегда. Ответ на вопрос о независимости смешанных вторых производных от порядка дифференцирования функции двух переменных дает следующая теорема. ТЕОРЕМА 1. Если функция z = f(x, у) дважды дифференцируема в точке М0(x0, y0), тo ее смешанные производные в этой точке равны.
Поиск по сайту: |
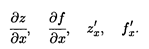





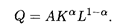

 в точке М.
в точке М. 

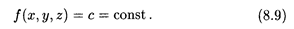
 в точке М (0, 1).
в точке М (0, 1).