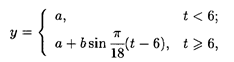|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Несобственные интегралы
При рассмотрении определенного интеграла как предела интегральных сумм предполагалось, что подынтегральная функция, во-первых, задана на конечном отрезке и, во-вторых, ограничена. Данное выше определение определенного интеграла не имеет смысла при невыполнении хотя бы одного из этих условий. Нельзя разбить бесконечный интервал на конечное число отрезков конечной длины; при неограниченной функции интегральная сумма не имеет предела. Тем не менее возможно обобщить понятие определенного интеграла и на эти случаи, с чем и связано понятие несобственного интеграла. Определение. Пусть функция f(x) определена на промежутке [а, +
имеет смысл. Предел этого интеграла при R
Если этот предел конечен, говорят, что несобственный интеграл (7.16) сходится, а функцию f(x) называют интегрируемой на бесконечном промежутке [а, Аналогичным образом вводится понятие несобственного интеграла по промежутку (-
Наконец, несобственный интеграл с двумя бесконечными пределами можно определить как сумму несобственных интегралов (7.16) и (7.17):
где с — любое число. Геометрический смысл несобственного интеграла первого рода заключается в следующем: это площадь бесконечной области (рис. 7.8), ограниченной сверху неотрицательной функцией f(x), снизу — осью Оx, слева — прямой х = а.
Рассмотрим несколько примеров несобственных интегралов.
Здесь пришлось разделить исходный интеграл на два и к каждому из них применить определение несобственного интеграла. Пример 4. Решение. Рассмотрим разные случаи для числа α. 1. При α = 1 для любого R > 0 имеем
т.е. конечного предела не существует и несобственный интеграл расходится. 2. При α ≠ 1 для любого R > 0 получаем
Следовательно, данный интеграл сходится при α > 1 и расходится при α ≤ 1. В приведенных выше примерах сначала с помощью первообразной вычислялся интеграл по конечному промежутку, а затем осуществлялся переход к пределу. Между тем если для функции f(x) существует первообразная F(x) на всем промежутке интегрирования [а,
Отсюда следует, что несобственный интеграл существует (сходится) в том и только в том случае, когда существует конечный предел
и тогда можно записать:
Аналогичный вывод справедлив и для несобственных интегралов вида (7.17) и (7.18):
Иными словами, формула Ньютона-Лейбница (основная формула интегрального исчисления) применима и в случае, когда пределы интегрирования бесконечны. УПРАЖНЕНИЯ
Вычислить определенные интегралы.
Найти площади фигур, ограниченных следующими линиями.
Найти объемы тел, образованных вращением вокруг оси Ох фигуры, ограниченной следующими линиями.
Вычислить несобственные интегралы в случае их сходимости.
7.32. Найти площадь, заключенную между кривой у = 7.33. Найти объем тела, образованного вращением вокруг оси Ох дуги кривой у = e-x от х = 0 до х = +
Решить задачи с экономическим содержанием. 7.34. Найти стоимость перевозки М т груза по железной дороге на расстояние 1 км при условии, что тариф у перевозки одной тонны убывает на а р. на каждом последующем километре. 7.35. Мощность у потребляемой городом электроэнергии выражается формулой
где t — текущее время суток. Найти суточное потребление электроэнергии при а = 15000 кВт, b = 12000 кВт.
Поиск по сайту: |
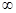 ) и интегрируема на любом отрезке [a, R], R > 0, так что интеграл
) и интегрируема на любом отрезке [a, R], R > 0, так что интеграл
 называется несобственным интегралом с бесконечным пределом интегрирования:
называется несобственным интегралом с бесконечным пределом интегрирования:
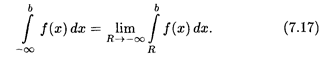




 , где α — некоторое положительное число.
, где α — некоторое положительное число.
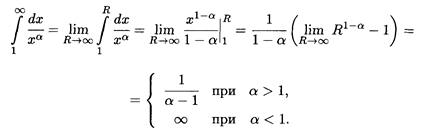






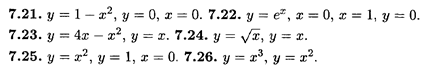
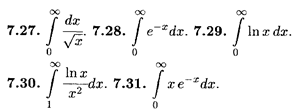
 и ее асимптотой при х ≥ 0.
и ее асимптотой при х ≥ 0.