|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Исследование функций и построение графиков
Признак монотонности функции
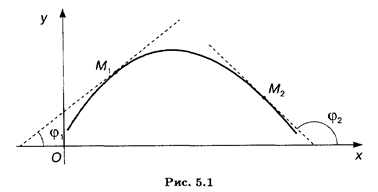
Одной из существенных характеристик функции является ее поведение на отдельных интервалах — возрастание или убывание. Это определяется приводимой ниже теоремой, доказательство которой мы опускаем. ТЕОРЕМА 2. Если функция f (x) дифференцируема и f'(x) ≥ 0 (f'(x) ≤ 0) на интервале (а, b), то она не убывает (не возрастает) на этом интервале. При f'(x) > 0 (f'(x) < 0) имеем признак строгой монотонности, т.е. функция возрастает (убывает). Геометрическая интерпретация связи знака производной функции и характера ее изменения очевидна (рис. 5.1): если углы наклона касательных на каком-то интервале являются острыми, то функция на этом интервале возрастает: tg φ > 0; при тупом угле наклона касательной функция убывает и tg φ < 0.
Точки локального экстремума Определение 1. Точка x0 называется точкой локального максимума (минимума) функции f(x), если для любого х ≠ x0 в некоторой окрестности точки x0 выполнено неравенство f(x0) > f(х) (f(x0) < f(x)). Локальный минимум и локальный максимум объединены общим названием локальный экстремум. ТЕОРЕМА 3 (необходимое условие существования локального экстремума). Если функция f(x) дифференцируема в точке x0 и имеет в этой точке локальный экстремум, то f'(x0) = 0. Геометрический смысл теоремы 5.3 указан на рис. 5.2: если в точках локальных экстремумов существуют касательные, то они параллельны оси Ох. Точки, в которых касательные параллельны оси Оx, а значит, производная равна нулю, называют точками возможного экстремума, или стационарными точками. Если x0 — точка возможного экстремума, т.е. f'(x0) = 0, то она может ине быть точкой локального экстремума. Например, для функции f(x) = x3 (рис. 3.1) производная при х = 0 равна нулю, однако в этой точке нет локального экстремума. Таким образом, теорема 5.3 не является достаточным условием существования локального экстремума.
ТЕОРЕМА 4 (достаточное условие существования локального экстремума). Пусть функция f(x) дифференцируема в некоторой окрестности точки x0. Если при переходе через точку x0 слева направо производная f'(x) меняет знак с плюса на минус (с минуса на плюс), то в точке x0 функция f(x) имеет локальный максимум (минимум). Если же f'(x) не меняет знака в δ-окрестности точки x0, то данная функция не имеет локального экстремума в точке x0. Рассмотрим применение доказанных теорем на примерах нахождения точек локальных экстремумов функций. Пример 1. Найти точки локального экстремума и интервалы монотонности функции f(x) = х3 — 7,5x2 + 18x. Решение. Сначала находим производную f'(x) = 3x2 — 15x + 18. Приравнивая ее к нулю и решая уравнение х2 — 5х + 6 = 0, находим две точки возможного экстремума: x1 = 2 и x2 = 3. Нетрудно видеть, что f'(x) при переходе через точку x1 =2 меняет знак с "+" на "-", т.е. в этой точке имеет место локальный максимум; аналогично устанавливается, что в точке x2 = 3 функция f'(х) имеет локальный минимум. Найдем теперь интервалы монотонности данной функции (рис. 5.3). Поскольку f'(x) > 0 при х
Пример 2. Найти размеры консервной банки, имеющей форму цилиндра (радиус r и высоту h) заданного объема V, при которых полная поверхность сосуда будет минимальной. Эта задача имеет производственный смысл: найти оптимальные размеры банки, при которых затраты материала на ее изготовление будут минимальны. Решение. Исходя из формулы объема цилиндра V = πr2h, выразим h:
Как известно, полная поверхность цилиндра дается формулой
Подставляя сюда формулу для h, получаем S как функцию от r:
Минимум этой функции найдем из условия S' (r) = 0, откуда получаем уравнение 2r — V / π r2 = 0. Из этого уравнения находим оптимальное значение r; его подставляем в формулу для h и окончательно вычисляем оптимальные размеры банки:
Например, при V = 0,33 л оптимальные размеры банки составят: диаметр дна ≈ 7,5 см и высота ≈ 7,5 см. Выпуклость и точки перегиба графика функции Определение 2. Будем говорить, что график функции y = f(x) имеет на интервале (а, b) выпуклость, направленную вниз (вверх), если он расположен не ниже (не выше) любой касательной к графику функции на (а, b) (рис. 5.4).
Способ определения направления выпуклости графика функции дается теоремой, приведенной ниже без доказательства.
ТЕОРЕМА 5. Если функция у = f(х) имеет на интервале (а, b) вторую производную и f"(x) ≥ 0 (f"(x) ≤ 0) на (а, b), то график функции имеет на (а, b) выпуклость, направленную вниз (вверх). Определение 3. Точка М(x0, f(x0)) называется точкой перегиба графика функции у = f(x), если в точке М график имеет касательную и существует такая окрестность точки x0, в пределах которой график функции f(x) имеет разные направления выпуклости. В точке перегиба касательная пересекает график функции, поскольку он переходит с одной стороны касательной на другую, т.е. "перегибается" через нее (рис. 5.5).
ТЕОРЕМА 6. (необходимое условие существования точки перегиба). Пусть график функции у = f(x) имеет перегиб в точке M(x0, f(x0)) и функция f(x) имеет в точке x0 непрерывную вторую производную. Тогда
Отметим, что не всегда условие f"(x0) = 0 означает наличие точки перегиба на графике функции у = f(x). Например, график функции у = x2n (п > 1) не имеет перегиба в точке (0, 0), хотя при х = 0 вторая производная равна нулю. Потому равенство (5.8) является только необходимым условием перегиба. Точки графика, для которых условие (5.8) выполнено, будем называть критическими. В каждой такой точке необходимо исследовать дополнительно вопрос о наличии перегиба; здесь имеется полная аналогия с существованием экстремума функции.
ТЕОРЕМА 7 (достаточное условие существования точки перегиба). Пусть в некоторой окрестности точки x0 вторая производная функции у = f(x) имеет разные знаки слева и справа от x0. Тогда график у = f(x) имеет перегиб в точке М(x0, f(x0)).
Теорема верна и для случая, когда f"(x) существует в некоторой окрестности точки x0 за исключением самой точки x0 и существует касательная к графику функции в точке М. Например, функция f(x) = x1/3 в точке х = 0 имеет бесконечные производные; в точке O(0, 0) касательная совпадает с осью Оу. Однако график этой функции имеет перегиб в начале координат, поскольку вторая производная f"(x) = -2 /(9x5/3) имеет разные знаки слева и справа от точки х = 0 (рис. 5.6). Рассмотрим примеры: найти точки перегиба и направления выпуклости графиков следующих функций.
Пример 3. f(x) = ехр (-x2). Решение. Последовательно находим f'(x)= -2x exp(—x2), f"(x) = 2 exp (-x2)(2x2 — 1). Приравнивая вторую производную к нулю, получаем критические точки х = ±1/
Пример 4. f(x) = ln (х2 – 2x + 2). РHешение. Вторая производная равна
Асимптоты графика функции
Часто оказывается, что график функции неограниченно приближается к некоторой прямой. Такого рода прямые называются асимптотами. Неограниченность приближения графика функции к асимптоте означает, что расстояние от графика до этой прямой (перпендикуляр, опущенный из произвольной точки графика на прямую) стремится к нулю. Различают три вида асимптот: вертикальные, горизонтальные и наклонные. Определение 4. Прямая х = а называется вертикальной асимптотой графика функции у = f(x), если хотя бы одно из предельных значений Вертикальные асимптоты обычно сопутствуют точкам разрыва второго рода. Например, график функции у = е1/x имеет вертикальную асимптоту х = 0, так как f(x) Определение 5. Прямая у = kx + b называется наклонной асимптотой графика функции у = f(x) при х
где α(х) Это определение относится как к наклонной, так и к горизонтальной асимптотам: в случае горизонтальной асимптоты угловой коэффициент k в (5.9) равен нулю. Укажем способ нахождения коэффициентов k и b в уравнении наклонной асимптоты. Разделив обе части равенства (5.9) на x и перейдя к пределу при х
т.е. k =
Рассмотрим примеры: найти асимптоты графиков функций.
Пример 5. f(x) = Решение. Найдем вертикальную асимптоту. Точка x = -1 является точкой разрыва 2-го рода, причем
Затем находим наклонные асимптоты:
Таким образом, получаем уравнение наклонной асимптоты
Пример 6. f(x) = х + e-x. Решение. Вертикальных асимптот здесь нет, поскольку точки разрыва 2-го рода отсутствуют. Отыщем наклонную асимптоту:
Таким образом, уравнение наклонной асимптоты имеет вид
Схема исследования графика функции
Приведем схему исследования поведения функции и построения ее графика. 1. Найти область определения функции. 2. Определить возможный тип симметрии функции: четность или нечетность функции. Функция f(x) называется четной, если выполнено условие симметрии ее графика относительно оси Оу:
Функция f(x) называется нечетной, если выполнено условие симметрии ее графика относительно начала координат O (0, 0):
При наличии симметрии достаточно построить график функции на правой координатной полуплоскости и затем отобразить его на левую половину: зеркально относительно оси Оу в случае (5.10) (рис. 5.8,а) или с центральной симметрией в случае (5.11) (рис. 5.8,6).
3. Найти точки пересечения графика функции с осями координат Ох и Оу, т.е. решить соответственно уравнения у = f(0) и f(x) = 0. 4. Найти асимптоты. 5. Найти точки возможного экстремума. 6. Найти критические точки. 7. Исследовать знаки первой и второй производных, определить участки монотонности функции, направление выпуклости графика, точки экстремума и перегиба. 8. Определить максимум и минимум функции на области ее определения. Если областью определения функции является отрезок [а, b], необходимо вычислить значения функции в его концах и сопоставить их с локальными экстремумами. 9. Построить график функции с учетом проведенного исследования. Пример 7. Исследовать и построить график функции
Решение. Действуем по приведенной выше схеме. 1. Область определения функции: х ≠ 0 или х 2. Функция (5.12) является нечетной, так как f(-x) = - f(x). 3. Уравнение f(x) = 0 дает корни х = ±1 (точки пересечения с осью Ох). Пересечения с осью Оу нет в силу п.1. 4. Имеется вертикальная асимптота — ось Оу, так как предел f(x) при х Определяем наклонную асимптоту:
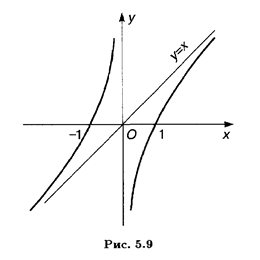
Итак, уравнение наклонной асимптоты: у = х. 5. f'(x) = 6. f"(x) = —2/х3 — критических точек нет. 7. Функция (5.12) монотонно возрастает на всей области своего определения, так как ее производная всюду положительна. В левой координатной полуплоскости выпуклость графика функции направлена вниз (f"(x) > 0), в правой полуплоскости выпуклость направлена вверх (f"(x) < 0). 8. Наибольшего и наименьшего значений функции не существует, поскольку область ее значений неограничена. 9. График функции (5.12) приведен на рис. 5.9.
Поиск по сайту: |

 (-
(- 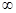 ,2), то в силу теоремы 5.2 функция монотонно возрастает на этом интервале; (2, 3) является интервалом монотонного убывания f(x) (f'(x) < 0), а на интервале (3, +
,2), то в силу теоремы 5.2 функция монотонно возрастает на этом интервале; (2, 3) является интервалом монотонного убывания f(x) (f'(x) < 0), а на интервале (3, + 








 . Ввиду зависимости функции от х2 достаточно исследовать точку x = l/
. Ввиду зависимости функции от х2 достаточно исследовать точку x = l/ 
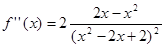 . Приравнивая ее к нулю, получаем критические точки x1 = 0, x2 = 2. Несложный анализ квадратного трехчлена х(2 — х), стоящего в числителе второй производной и определяющего ее знак, показывает, что точка перегиба M1 (0, ln 2) графика функции меняет выпуклость вверх слева на выпуклость вниз справа; в другой точке перегиба М2 (2, ln2) выпуклость графика функции вниз слева меняется на выпуклость вверх справа.
. Приравнивая ее к нулю, получаем критические точки x1 = 0, x2 = 2. Несложный анализ квадратного трехчлена х(2 — х), стоящего в числителе второй производной и определяющего ее знак, показывает, что точка перегиба M1 (0, ln 2) графика функции меняет выпуклость вверх слева на выпуклость вниз справа; в другой точке перегиба М2 (2, ln2) выпуклость графика функции вниз слева меняется на выпуклость вверх справа.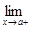 f(x) или
f(x) или  f(x) равно +
f(x) равно + 

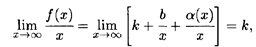
 . Затемиз равенства (5.9) находим:
. Затемиз равенства (5.9) находим:
 .
.









 (0,
(0, 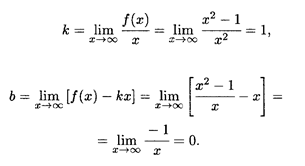
 , т.е. производная нигде не равна нулю и точек возможного экстремума нет. В области определения везде f'(x) положительна.
, т.е. производная нигде не равна нулю и точек возможного экстремума нет. В области определения везде f'(x) положительна.