 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Локальный экстремум функции нескольких переменных
Определение и необходимые условия существования локального экстремума
Пусть функция z = f(x, y) определена на множестве {М}, а М0 (x0, у0) — некоторая точка этого множества. Определение. Функция z = f(x, у) имеет в точке М0 локальный максимум (минимум), если существует такая окрестность точки M0, принадлежащая {М}, что для любой точки М(х, у) из этой окрестности выполняется неравенство f(M) ≤ f(M0) (f(М) ≥ f(М0)); для случая функции трех и более переменных локальный экстремум определяется аналогично. Согласно данному определению локального экстремума (минимума или максимума) полное приращение функции z = f(M) — f(М0) удовлетворяет одному из условий в окрестности точки M0: Δz ≤ 0, если M0 — точка локального максимума; Δz ≥ 0, если M0 — точка локального минимума. Теперь установим необходимые условия существования локального экстремума. ТЕОРЕМА 2. Если функция z = f(x, у) имеет в точке M0 (x0, y0) локальный экстремум и частные производные первого порядка, то все эти частные производные равны нулю:
Для случая функции двух и более переменных необходимое условие существования локального экстремума имеет вид, аналогичный (8.10); все частные производные первого порядка должны обращаться в нуль в точке M0. Следует особо отметить, что условия (8.10) не являются достаточными условиями экстремума. Например, для функции z = х2 — у2 частные производные равны нулю в точке O(0, 0), однако в этой точке функция (которая является уравнением гиперболического параболоида) не имеет экстремума: f(0, 0) = 0, но в любой окрестности точки О есть значения функции как положительные, так и отрицательные. Точки, в которых выполняются условия (8.10), называются точками возможного экстремума, или стационарными точками. Рассмотрим задачи на отыскание возможного экстремума функций.
Ррешение. Согласно условиям (8.10) имеем
Решение этой системы х = 1, у = 2, т.е. точка с координатами (1, 2) является стационарной для данной функции двух переменных.
Решение. По условию (8.10) все три первые частные производные функции равны в этой точке нулю, откуда получаем систему трех линейных алгебраических уравнений с тремя неизвестными
Решение этой системы дает единственную стационарную точку возможного экстремума: (3, -4, 2).
Достаточные условия существования локального экстремума
Рассмотрим случай функции двух переменных z = f(x, y), часто используемый на практике. Обозначим вторые частные производные этой функции ТЕОРЕМА 3. Пусть в точке М0(х0, у0) возможного экстремума функции и = f(x, у) и в некоторой ее окрестности все вторые частные производные этой функции непрерывны. Тогда если
то функция и = f(x, y) имеет в точке М0 локальный экстремум: минимум при а11 < 0 и максимум при а11 > 0. Если же а11а22 — a122 ≤ 0, то данная функция не имеет локального экстремума в точке M0. Пример 3. Найти точки локального экстремума и значения в них функции z = х3 — у3 — 3ху. Решение. Сначала находим стационарную точку из условий
решения которой дают координаты двух точек (0, 0) и (-1, 1). Найдем вторые производные:
откуда получаем Δ = а11a22 — а122 = -36xу — 9. В точке (0, 0) имеем Δ < 0, и, значит, в ней нет локального экстремума. В точке (-1, 1) получаем Δ = 27 > 0, т.е. в этой точке данная функция имеет локальный экстремум; поскольку а11 < 0, то это точка максимума. Значение функции в ней: umax = f(-1, 1) = 1.
Поиск по сайту: |


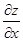 = 0 и
= 0 и  = 0, откуда получаем систему двух алгебраических уравнений с двумя неизвестными
= 0, откуда получаем систему двух алгебраических уравнений с двумя неизвестными


 ,
,  ,
, 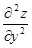 в некоторой точке M0 через а11, a12, a22 соответственно. Тогда достаточное условие локального экстремума формулируется следующим образом.
в некоторой точке M0 через а11, a12, a22 соответственно. Тогда достаточное условие локального экстремума формулируется следующим образом.

