 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Основные свойства определенного интеграла
1. Интеграл По определению полагаем
как определенный интеграл на отрезке нулевой длины. Также по определению полагаем, что
поскольку при движении от b к а все длины частичных отрезков Δxi = xi-1 — xi имеют отрицательный знак в интегральной сумме (7.1). 2. Для любых чисел а, b и с имеет место равенство
3. Постоянный множитель можно выносить за знак определенного интеграла:
4. Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их определенных интегралов:
Заметим, что свойство 4 имеет место для любого конечного числа слагаемых. Будем полагать далее, что а < b. 5. Если функция f(x) ≥ 0 всюду на отрезке [а, b], то
6. Если f(x) ≤ g(х) всюду на отрезке [а, b], то
7. Если функция f(x) интегрируема на [а, b], то
8. Если М и т — соответственно максимум и минимум функции f(x) на отрезке [а, b], то
Основная формула интегрального исчисления ТЕОРЕМА 4. Непрерывная на отрезке [а, b] функция f(x) имеет на этом отрезке первообразную. Одной из первообразных является функция
В формуле (7.8) переменная интегрирования обозначена буквой t, чтобы избежать путаницы с верхним переменным пределом х. Поскольку всякая другая первообразная отличается от F(x) на постоянную величину, то связь между неопределенным и определенным интегралами имеет вид
где С — произвольная постоянная. Согласно теореме 7.4 непрерывная на отрезке [а, b] функция f(x) имеет первообразную, которая определяется формулой
где С — некоторая постоянная. Подставляя в (7.9) х = а, с учетом свойства 1 определенного интеграла получаем
Тогда из (7.9) имеем
Полагая х = b, получаем формулу
Равенство (7.10) называется основной формулой интегрального исчисления, или формулой Ньютона-Лейбница. Разность F(b) — F(a) условно записывают символом F(x)
Формула (7.11) дает широкие возможности вычисления определенных интегралов. Нужно вычислить неопределенный интеграл и затем найти разность значений первообразной согласно (7.11). Рассмотрим примеры вычисления определенных интегралов.
Основные правила интегрирования
Поиск по сайту: |
 был определен для случая, когда a < b. Обобщим понятие определенного интеграла и на другие случаи.
был определен для случая, когда a < b. Обобщим понятие определенного интеграла и на другие случаи.

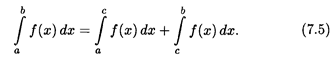












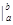 , т.е.
, т.е.
