 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Понятие сложной функции
Определение. Если на некотором промежутке Х определена функция z = φ(x) с множеством значений Z и на множестве Z определена функция у = f(z), то функция у = f[φ(x)] называется сложной функцией от x (или суперпозицией функций), а переменная z — промежуточной переменной сложной функции. Приведем примеры сложных функций. Пример 1.у = cos Пример 2. у = Пример 3. у= ТЕОРЕМА 8. Пусть функция z = φ(x) непрерывна в точке x0, а функция у = f(z) непрерывна в точке z0 = φ(x0). Тогда сложная функция у = f[φ{x)] непрерывна в точке x0 = 0. Пример 4. Функция y = tg (x2 + 2x) непрерывна в точке x = 0, так как функция z = х2 + х непрерывна в точке х = 0, а функция у = tg z непрерывна в точке z = 0.
Элементы аналитической геометрии на плоскости
Уравнение линии на плоскости
Пусть на плоскости задана система координат. Рассмотрим уравнение вида
Говорят,что уравнение (3.9) определяет (задает) линию L в системе координат Оху. Вообще говоря, линии на координатной плоскости могут быть самыми различными.
Линии первого порядка
К линиям первого порядка относятся те линии, для которых задающее их уравнение (3.9) содержит переменные x и у только в первой степени. Иными словами, такие линии описываются уравнениями вида
где А, В и С — постоянные числа. Из этого уравнения можно выразить переменную у как функцию от аргумента х при В ≠ 0:
Уравнение (3.11) называют уравнением прямой с угловым коэффициентом k = tg φ, где φ — угол наклона прямой к положительному направлению оси Ох (рис. 3.9). Если k = 0, то прямая параллельна оси Ох и отстоит от нее на b масштабных единиц.
Рис. 3.9
Определим самые необходимые элементы знания о прямых на плоскости. 1. Кроме "классического" уравнения прямой (3.11) следует знать еще две его разновидности. Первая из них — это уравнение прямой с заданным угловым коэффициентом k, проходящей через заданную точку М0(x0, у0):
Другой вид — это уравнение прямой, проходящей через две заданные точки на плоскости M1(x1, y1) и М2(х2, у2):
2. Угол между прямыми. Рассмотрим две прямые, заданные уравнениями у = k1x + b1 и у = k2x + b2, где k1 = tg φ1 и k2 = tg φ2 (рис. 3.10). Пусть φ — угол между этими прямыми. Тогда φ = φ2 — φ1 и мы получаем tg φ = tg (φ2 — φ1) =
Рис. 3.10
Формула (3.12) определяет один из углов между пересекающимися прямыми; второй угол равен π - φ. Из равенства (3.12) вытекают условия параллельности и перпендикулярности прямых. В самом деле, если прямые параллельны, то
Если прямые перпендикулярны, то α2 = π/2 + α1, откуда tg α2 = -ctg α1 = -1 / tg α1, или окончательно
Пример 1. Найти угол между прямыми, заданными уравнениями у = 2x - 5 и у = -3x + 4. Решение. Подставляя в формулу (3.12) значения k1 = 2 и k2 = -3, имеем
откуда получаем, что один из углов равен φ = π / 4. 3. Расстояние от точки до прямой. Пусть прямая задана уравнением общего вида (3.10). Тогда расстояние dотпроизвольной точки М0(x0, y0) до прямой (рис. 3.11)даетсяформулой
Рис. 3.11 Линии второго порядка Рассмотрим здесь три наиболее используемыxвида линий:эллипс, гиперболу и параболу. 1. Эллипс. Линия, для всех точек которой сумма расстояний от двух данных точек, называемых фокусами, есть величина постоянная и большая, чем расстояние между фокусами, называется эллипсом. Согласно определению эллипса, сумма расстояний от произвольной точки М на этой линии до его фокусов F1 и F2 постоянна (рис. 3.12):
Рис. 3.12
Отсюда можно вывести уравнение эллипса в его основной (канонической) форме:
где а и b — полуоси эллипса, b2 = а2 — с2, точка O (0,0) — центр эллипса, с — половина расстояния между фокусами эллипса. Из уравнения (3.13) следует, что оси эллипса являются его осями симметрии, а точка их пересечения — центром его симметрии.
В частном случае, когда a = b, фокусы эллипса сливаются, т.е. с = 0, и мы имеем окружность радиуса а с центром в начале координат. Характеристикой эллипса, показывающей меру его вытянутости, является эксцентриситет — величина, определяемая отношением
2. Гипербола. Гиперболой называется линия, для всех точек которой модуль разности расстояний от двух данных точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами. На рис. 3.13 показаны все основные элементы гиперболы. Разность расстояний от произвольной точки М на гиперболе до фокусов F1 и F2, согласно определению, есть величина постоянная:
Из этой основной предпосылки выводится каноническое уравнение гиперболы, которое имеет вид
где b2 = с2 — а2. Нетрудно видеть, что прямые у = ± 3. Парабола. Параболой называется линия, все точки которой находятся на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус. Согласно определению, точка М(х, у) лежит на параболе, если r1 = r2. Отсюда и выводится каноническое уравнение параболы, которое имеет вид
График параболы (3.15) показан на рис. 3.14. Нетрудно видеть, что перемена осей координат приводит к более привычному уравнению параболы вида у = Ах2, где А — постоянное число.
Рис. 3.14 УПРАЖНЕНИЯ
Найти области определения функций, заданных следующими формулами. 3.1. у = 3x - 2.3.2. у = х2 – 5x + 6.3.3. 3.15.f(x) = x2 + x – 2, найти f(0), f(1), f(-3).3.16.f(x)=arccos(lg x), найти f(1/10), f(1), f(10).3.17. 3.18. Спрос и предложение на некоторый товар на рынке описываются линейными зависимостями вида
1) Определить равновесную цену; 2) установить графическим способом, является ли модель паутинного рынка "скручивающейся". Варианты задания параметров зависимостей спроса и предложения: а) а = 19, b = 2, с = 3, d = 2; б) а = 15, b = 3, с = 1, d = 4;в)а = 11, b = 3, с = 3, d = 1; г) а = 23, b = 3, с = 5, d = 6.
Найти пределы.
3.19.
Найти точки разрыва функций и определить типы разрывов. 3.34.
Поиск по сайту: |
 —сложная функция, определенная на полубесконечном интервале (—
—сложная функция, определенная на полубесконечном интервале (—  ,1], так как у = f(z) = cos z, z = φ(x) =
,1], так как у = f(z) = cos z, z = φ(x) =  — сложная функция, определенная на всей числовой прямой, поскольку у = f(z) = еz , z = φ(x) = —х2.
— сложная функция, определенная на всей числовой прямой, поскольку у = f(z) = еz , z = φ(x) = —х2. — сложная функция, определенная на полубесконечных интервалах (-
— сложная функция, определенная на полубесконечных интервалах (- 





 или, что то же самое,
или, что то же самое,



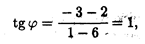









 х являются наклонными асимптотами гиперболы. Линия (3.14) имеет две оси симметрии, точка пересечения которых является центром симметрии гиперболы.
х являются наклонными асимптотами гиперболы. Линия (3.14) имеет две оси симметрии, точка пересечения которых является центром симметрии гиперболы.

 . 3.4.
. 3.4.  . 3.5.
. 3.5.  . 3.6.
. 3.6.  . 3.7.
. 3.7.  . 3.8.
. 3.8.  . 3.9.
. 3.9.  . 3.10.
. 3.10.  . 3.11.
. 3.11.  . 3.12.
. 3.12.  . 3.13.
. 3.13.  . 3.14.
. 3.14.  .
. .
.
 . 3.20.
. 3.20.  . 3.21.
. 3.21.  . 3.22.
. 3.22.  . 3.23.
. 3.23.  . 3.24.
. 3.24.  . 3.25.
. 3.25.  . 3.26.
. 3.26.  . 3.27.
. 3.27.  . 3.28.
. 3.28.  . 3.29.
. 3.29.  . 3.30.
. 3.30.  . 3.31.
. 3.31. 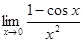 . 3.32.
. 3.32.  . 3.33.
. 3.33.  .
. .3.35.
.3.35.  .3.36.
.3.36.  . 3.37.
. 3.37.  .3.38.
.3.38.  .3.39.
.3.39.  .3.40.
.3.40.  .
.