 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Непрерывность элементарных функций
Непрерывность элементарных функций в точке
Постоянная функция f(x) = С является непрерывной в любой точке числовой прямой. Действительно, Функция f(x) = х непрерывна в каждой точке а числовой прямой, так как предел функции в точке а равен еезначению в этой точке: Из сказанного выше и теоремы 3.7 следует, что в любой точке числовой прямой функции x2 = x ∙ x, x3 = x2 ∙ х,..., xn = xn-1 ∙ x (n — натуральное число) непрерывны. Алгебраический многочлен
также является непрерывной функцией в любой точке числовой прямой в силу теоремы 3.7, поскольку представляет собой сумму произведений непрерывных функций. Дробно-рациональная функция
где Р(x) и Q(x) — алгебраические многочлены, в силу теоремы 3.7 непрерывна во всех точках числовой прямой за исключением корней знаменателя. Тригонометрические функцииsin x, и cos x непрерывны в любой точке x числовой прямой. Непрерывность функций tg x = sin x / cos x и sec x = 1/ cos x соблюдается во всех точках, x ≠ π / 2 + nπ; аналогично непрерывность функций ctg x = cos x / sin x и sec x = 1 / sin x обеспечена во всех точках x ≠ пπ (n = 0, ±1, ±2,...). Рассмотренные выше функции непрерывны в каждой точке, в окрестности которой они определены. В силу теоремы 3.7 функции, получаемые из них при использовании конечного числа арифметических операций, являются также непрерывными.
Непрерывность функции на интервале и отрезке
Говорят, что функция f(x) непрерывна на интервале (а, b), если она непрерывна в каждой точке этого интервала. Функция f(x) непрерывна на отрезке [а, b], если она непрерывна на интервале (а, b) и непрерывна в точке a справа, а в точке b слева:
Классификация точек разрыва функции
Точки разрыва, в которых функция не является непрерывной, классифицируются следующим образом. 1. Устранимый разрыв.Точка а называется точкой устранимого разрыва функции f(x), если предел функции в этой точке существует, но в точке а функция f(x) либо не определена, либо ее значение f(а) не равно пределу в этой точке.
Пример 1. Функция f(x) =
Функция f1(x) является непрерывной на всей числовой прямой. 2. Разрыв первого рода. Точка а называется точкой разрыва первого рода функции f(x), если в этой точке функция имеет конечные, но не равные друг другу левый и правый пределы:
Пример 2. Рассмотрим функцию
для нее точка х = 0 является точкой разрыва 1-го рода. 3. Разрыв второго рода. Точка а называется точкой разрыва второго рода функции f(x), если в этой точке функция f(x) не имеет по крайней мере одного из односторонних пределов или хотя бы один из односторонних пределов бесконечен. Пример 3. Для функции f(x) = 1/x точка х = 0 является точкой разрыва 2-го рода, поскольку Пример 4. Для функции f(x) = sin (l/x) точка х = 0 является точкой разрыва 2-го рода, так как ни левого, ни правого предела функции в этой точке не существует. Пример 5. Рассмотрим функцию f(x) = е1/x = ехр
Рис. 3.8
Поиск по сайту: |
 f(x) = С = f(а), что соответствует определению непрерывности функции в точке.
f(x) = С = f(а), что соответствует определению непрерывности функции в точке.


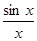 в точке х = 0, как известно, имеет предел, равный единице (первый замечательный предел). Однако в самой точке х = 0 эта функция не определена, т.е. здесь разрыв первого вида. Этот разрыв можно устранить (потому он и называется устранимым), если доопределить функцию в этой точке значением предела в ней, т.е. ввести новую функцию
в точке х = 0, как известно, имеет предел, равный единице (первый замечательный предел). Однако в самой точке х = 0 эта функция не определена, т.е. здесь разрыв первого вида. Этот разрыв можно устранить (потому он и называется устранимым), если доопределить функцию в этой точке значением предела в ней, т.е. ввести новую функцию
 .
.

 .
. (рис. 3.8). Точка х = 0 является точкой разрыва 2-го рода для этой функции, так как предел слева равен нулю, а предел справа бесконечен:
(рис. 3.8). Точка х = 0 является точкой разрыва 2-го рода для этой функции, так как предел слева равен нулю, а предел справа бесконечен:
