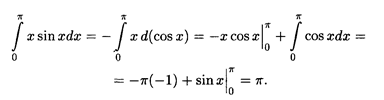Замена переменной в определенном интеграле

ТЕОРЕМА 5. Пусть: 1) f(x) — непрерывная функция на от­резке [а, b]; 2) функция φ(t) дифференцируема на [α, β], причем φ'(t) непрерывна на [α, β] и множеством значений функции φ(t) является отрезок [а, b], 3) φ(α) = а, φ(β) = b. Тогда справедлива формула

Формула (7.12) называется формулой замены переменной или подстановки в определенном интеграле.

Заметим, что при вычислении определенного интеграла с помощью замены переменной нет нужды возвращаться к преж­ней переменной, как это делалось при вычислении неопределен­ного интеграла, так как определенный интеграл представляет собой число, которое согласно формуле (7.12) равно значению каждого из рассматриваемых интегралов. Теперь при подста­новке следует сначала найти новые пределы интегрирования и затем выполнить необходимые преобразования подынтеграль­ной функции.

Заметим также, что при замене переменной в определенном интеграле необходимо соблюдать условия теоремы 7.5, иначе можно получить неверный результат (особое внимание следует уделять выполнению условия 2 теоремы).

Вычислить определенные интегралы методом подстановки.

Решение. Выполним подстановку t = 1 + х². Тогда dt = 2х dx, t = 1 при х = 0 и t = 2 при х = 1. Поскольку функция х = непрерывна на [1, 2], то и новая подынтегральная функция также непрерывна, и, значит, для нее в силу теоре­мы 7.5 существует первообразная на этом отрезке. Получаем

Решение. Применим здесь подстановку х = a sin t. Тогда dx = a cos t dt, = a cos t, t = arcsin , t = 0 при x = 0, t = при x = а. Подставляя все это в исходный интеграл, получим

Решение. По формуле Ньютона-Лейбница имеем

Вычислим этот интеграл при помощи замены переменной t = tg х. Тогда t = 0 при х = 0 и t = 0 при х = π, х = arctg t, т.е. dx = dt / (l + t²). Подстановка в исходный интеграл дает

Полученное противоречие объясняется тем, что функция за­мены переменной t = tg x имеет разрыв при х = π/2 и не удовлетворяет условию 2 теоремы 7.5.

Интегрирование по частям в определенном интеграле

ТЕОРЕМА 6. Пусть функции и(х) и v(x) имеют непрерывные производные на отрезке [а, b]; тогда справедлива формула

Равенство (7.13) называется формулой интегрирования по частям в определенном интеграле. Рассмотрим ряд приме­ров вычисления определенных интегралов методом интегриро­вания по частям.

Решение. Положим здесь и = х, v = e^-x, тогда dv = -e^-xdx и

Решение. Здесь и = х, sin x dx = dv или v = - cos x; далее по формуле (7.13) имеем

Геометрические приложения определенного интеграла

Поиск по сайту: