 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Глава 5. ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ В ИССЛЕДОВАНИИ ФУНКЦИЙ
L. Раскрытие неопределенностей
Правило Лопиталя
Будем говорить, что отношение двух функций
Раскрыть эту неопределенность означает вычислить предел ТЕОРЕМА 1 (теорема Лопиталя*). Пусть функции f(x) и g(х) определены и дифференцируемы в некоторой окрестности точки а за исключением, быть может, самой точки a. Кроме того, пусть
* Гийом Франсуа Антуан де Лопиталь — французский математик (1661 — 1704).
Эту теорему обычно называют правилом Лопиталя. Замечание 1. Правило Лопиталя можно применять повторно, если f'(x) и g'(х) удовлетворяют тем же требованиям, что и исходные функции f(x) и g(х). Замечание 2. Теорема остается верной и в случае, когда х Теперь рассмотрим примеры. Пример 1.
Здесь мы дважды последовательно применили правило Лопиталя, поскольку два раза имели дело с неопределенностью вида Пример 2.
Пример 3.
Неопределенности вида Будем называть отношение двух функций Пример 4.
Пример 5.
Другие виды неопределенностей
Неопределенности вида 0 ∙ Пример 6. Найти предел Решение. Здесь неопределенность вида 0 ∙
Пример 7. Найти Решение. Это неопределенность вида
Теперь это неопределенность вида
Рассмотрим неопределенности вида 00, 1
Пример 8. Найти предел Решение. Это предел вида 00; используя формулу (5.1), имеем с учетом решения шестого примера
Пример 9. Найти предел
Решение. Это предел вида 1
Следовательно, искомый предел равен
Формула Маклорена Разложение функций по формуле Маклорена
Одним из основных принципов математики является представление сложного через более простое. Формула Маклорена* как раз и является реализацией этого принципа. Любые функции, дифференцируемые достаточное число раз в точке х = 0, могут быть представлены в виде многочлена некоторой степени. Многочлены же являются наиболее простыми элементарными функциями, над которыми удобно выполнять арифметические действия, вычислять значения в любой точке и т.д. * Колин Маклорен — шотландский математик (1698 — 1746).
Итак, функцию f(x), имеющую (n + 1) производных в точке х = 0, можно представить по формуле Маклорена вместе с остаточным членом:
Формула (5.2) дает возможность разложить функцию f(x) по формуле Маклорена (в окрестности нуля) или, что то же самое, представить f(x) в виде многочлена, коэффициенты которого вычисляются достаточно просто. Эта формула широко используется и для приближенных вычислений значений различных функций; при этом погрешность вычислений оценивается по остаточному члену о(xn). Рассмотрим примеры разложения функций по формуле Маклорена. Пример 1. f(x) = еx. Решение. Поскольку (ex)(n) = eх, f(n)(0) = е0 = 1 для любого п, формула Маклорена (5.2) имеет вид
Формула (5.3) используется для вычисления числа е с любой необходимой точностью. Отсюда при х = 1 получаем приближенное значение числа е ≈ 2,7182818 .... Пример 2. f(x) = sin x. Решение. Нетрудно проверить, что f(n)(x) = sin
Подстановка в формулу (5.3) приводит к выражению
Пример 3. f(x) = cos x. Решение. По аналогии с функцией синуса имеем
Подстановка в формулу (5.2) приводит к разложению по формуле Маклорена:
Пример 4. f(x) = ln (l + х). Решение. Так как
Пример 5. f(x) = (1 + x)α, где α — вещественное число. Решение. Производная n-го порядка имеет вид f(n)(x) = α(α - 1)( α - 2)... (α - n +1)(1 + x) α-n, т.е. f(n)(0) = α(α — 1)... (α - п + 1), и формула Маклорена для данной функции такова:
В частном случае, когда α = п — целое число, имеем f(n + l) = 0 и формула (5.7) переходит в формулу бинома Ньютона:
т.е. бином Ньютона является частным случаем формулы Маклорена.
Формула Маклорена в асимптотических формулах и вычислениях пределов функций
Формулы (5.3)-(5.7) представляют собой асимптотические формулы (или оценки) соответственно для функций eх, sin x, cos x, ln (l + x), (1 + x) α при x
Пример 6. Найти Решение. Применяя формулу (5.2) при п = 2, получаем
Поиск по сайту: |
 при x
при x  a есть неопределенность вида
a есть неопределенность вида  , если
, если
 , если он существует.
, если он существует. , причем g'(х) ≠ 0 в указанной окрестности точки а. Тогда если существует предел отношения
, причем g'(х) ≠ 0 в указанной окрестности точки а. Тогда если существует предел отношения  (конечный или бесконечный), то существует и предел
(конечный или бесконечный), то существует и предел 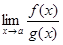 , причем справедлива формула
, причем справедлива формула
 (х
(х 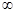 ).
).



 , -
, -  на условие
на условие 
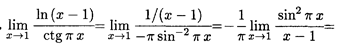

 x ln x.
x ln x. и теперь уже имеем неопределенность вида
и теперь уже имеем неопределенность вида 
 (cosec x — ctg x).
(cosec x — ctg x).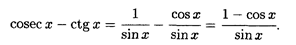

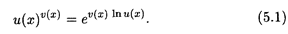
 .
.





 ; отсюда имеем
; отсюда имеем

 , откуда получаем
, откуда получаем

 , то f(0) = 0,
, то f(0) = 0,  ; подстановка в формулу (5.2) приводит к разложению функции ln (1 +x) по формуле Маклорена (при этом 0! = 1):
; подстановка в формулу (5.2) приводит к разложению функции ln (1 +x) по формуле Маклорена (при этом 0! = 1):


 .
.