 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Глава 8. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
8.1. Евклидово пространство Em
Евклидова плоскость и евклидово пространство
Как мы знаем, множество всех упорядоченных пар вещественных чисел (x, у) называется координатной плоскостью и каждая точка на ней характеризуется парой своих координат: М(x, у). Определение 1. Координатная плоскость называется евклидовой плоскостью, если расстояние между двумя любыми точками M1(x1, y1) и М2(x2, y2) определено по формуле
Аналогично вводится и понятие евклидова пространства. В этом случае каждая точка координатного пространства характеризуется тройкой чисел и тогда расстояние между двумя любыми точками пространства M(x1, y1 ,z1) и М(x2, y2, z2) определяется формулой
Стало быть, евклидова плоскость и евклидово пространство определяются способом измерения расстояния между двумя любыми своими точками.
Понятия m-мерного координатного пространства и m-мерного евклидова пространства Определение 2. Множество всевозможных упорядоченных совокупностей т действительных чисел (x1, х2, x3, ..., xm) называется т-мерным координатным пространством Аm. Каждую упорядоченную совокупность (x1, x2, x3,, … ,xт,) называют точкой этого пространства и обозначают одной буквой М. При этом числа x1, x2, x3, …, xm называются координатами точки М, что символически записывается следующим образом: М(x1, x2, ..., xm). Определение 3. Координатное пространство Аm называется т-мерным евклидовым пространством Еm, если между двумя любыми точками М'(х1', х2, '... , хm') и М"(x1'', х2'',... , хm'') пространства Аm определено расстояние ρ(М', М") по формуле
Очевидно, что введенные понятия m-мерного координатного пространства Аm и m-мерного евклидова пространства Em являются обобщениями понятий соответственно координатных плоскости и пространства и евклидовых плоскости и пространства.
8.2. Множества точек евклидова пространства Еm
Примеры множеств евклидова пространства Еm
Будем обозначать символом {М} некоторое множество точек m-мерного пространства Еm. Рассмотрим некоторые примеры множеств в этом пространстве. 1. Множество {М} всевозможных точек, координаты x1, x2, ..., xm которых удовлетворяют неравенству
называется т-мерным шаром радиуса R с центром в точке M0(x Этот пример является m-мерным обобщением соответственно круга на евклидовой плоскости и шара в трехмерном евклидовом пространстве, которые задаются следующими неравенствами:
Неравенство (8.2) можно переписать с учетом (8.1) в виде
В случае строгого неравенства ρ(М, М0) < R множество {М} называется открытым т-мерным шаром. Часто это множество также называют R-окрестностью точки M0. В случае (8.3) если неравенство не строгое, множество {М} называется замкнутым т-мерным шаром. Эти понятия переносятся на случай любой размерности при т ≥ 2. 2. Множество {М} точек, таких, что расстояние от каждой из них до некоторой точки M0 удовлетворяет равенству ρ(М, М0) = R, называется т-мерной сферой радиуса R с центром в точке M0. Аналогия: для плоскости — окружность (x – x0)2 + (у – y0)2 = R2 радиуса R с центром в точке М0(х0, у0), для пространства — сфера (x – x0)2 + (у – y0)2 + (z – z0)2 = R2 радиуса R с центром в точке М0(х0, у0, z0).
Понятие функции нескольких переменных
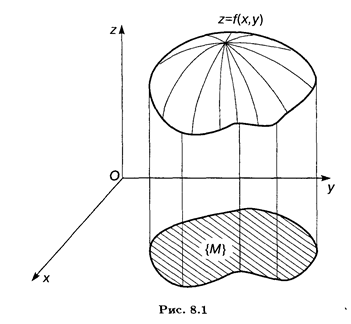
Введем понятие функции нескольких переменных. Определение 1. Пусть каждой точке М из множества точек {М} евклидова пространства Em по какому-либо закону ставится в соответствие некоторое число и из числового множества U. Тогда будем говорить, что на множестве {М} задана функция и = f(M). При этом множества {М} и U называются соответственно областью определения (задания) и областью изменения функции f(M). Как известно, функция одной переменной у = f(x) изображается на плоскости в виде линии. В случае двух переменных область определения {Мп} функции z = f(x, y) представляет собой некоторое множество точек на координатной плоскости Оху (рис. 8.1). Координата z называется аппликатой, и тогда сама функция изображается в виде некоторой поверхности в пространстве E3. Аналогичным образом функция от т переменных
определенная на множестве {М} евклидова пространства Еm, представляет собой гиперповерхность в евклидовом пространстве Еm+1.
Некоторые виды функций нескольких переменных
Рассмотрим примеры функций нескольких переменных и найдем их области определения.
Решение. Это поверхность в евклидовом пространстве Е3. Областью определения этой функции является все множество точек плоскости Оху. Область значений этой функции — промежуток [0,
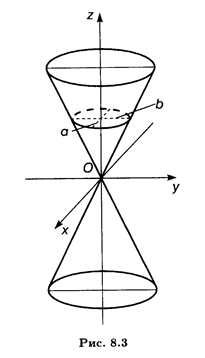
Решение. Это поверхность в евклидовом пространстве Е3. Область определения данной функции — все множество точек евклидова пространства Е2 или плоскости Оху. Эта функция является так называемым эллиптическим конусом с вершиной в начале координат O(0, 0, 0); приведенная формула суммирует две функции, задающие две его симметричные относительно плоскости Оху части (рис. 8.3):
Приведем теперь наиболее часто встречающиеся в различных приложениях виды функций нескольких переменных. 1. Уравнение вида
называется общим уравнением плоскости в системе координат Oxyz. Вектор
Например, составить уравнение плоскости с перпендикулярным вектором
2. Функция Кобба—Дугласа — производственная функция, показывающая объем выпуска продукции Q при затратах капитала К и трудовых ресурсов L. Для случая двух переменных она имеет вид
где А > 0 — параметр производительности конкретно взятой технологии, 0 < α < 1 — доля капитала в доходе.
Линии уровня
Понятие линии уровня широко используется прежде всего в геодезии, картографии, при составлении синоптических карт, а также при описании различных физических полей (температура, давление и пр.). Определение 2. Линией уровня функции двух переменных z = f(x, y) называется плоская кривая, получаемая при пересечении графика этой функции плоскостью z = С, где С — постоянная величина, параллельной координатной плоскости Оху. Обычно линии уровня, соответствующие различным значениям постоянной величины С, проецируются на одну плоскость, например на координатную плоскость Оху; тогда их удобно анализировать и с их помощью исследовать сложный характер поверхности, описываемой функцией z = f(x, у). Таким образом, можно сказать, что линии уровня функции z = f(x, у) — это семейство кривых на координатной плоскости Оху, описываемое уравнениями вида
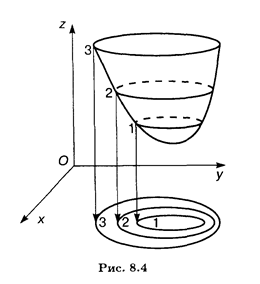
Обычно берут арифметическую прогрессию чисел Ci с постоянной разностью h; тогда по взаимному расположению линий уровня можно получить представление о форме поверхности, описываемой функцией z = f(x, у). Там, где функция изменяется быстрее, линии уровня сгущаются, а там, где поверхность пологая, линии уровня располагаются реже (рис. 8.4).
Пример 3. Найти линии уровня функции z = х2 + у2 — 2х — 2у. Решение. Линии уровня данной функции — это семейство кривых на плоскости Оху, описываемое уравнением
Последнее уравнение описывает семейство окружностей с центром в точке O1(l, 1) радиуса r =
Поиск по сайту: |
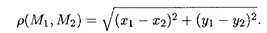
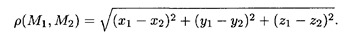


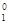 ,x
,x  ,...,x
,...,x 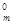 ).
).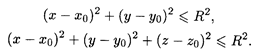

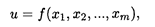

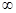 ). Данная функция представляет собой параболоид вращения (рис. 8.2): в вертикальных сечениях этой поверхности плоскостями Oxz и Оуz получаются соответственно параболы z = х2 и z = у2.
). Данная функция представляет собой параболоид вращения (рис. 8.2): в вертикальных сечениях этой поверхности плоскостями Oxz и Оуz получаются соответственно параболы z = х2 и z = у2.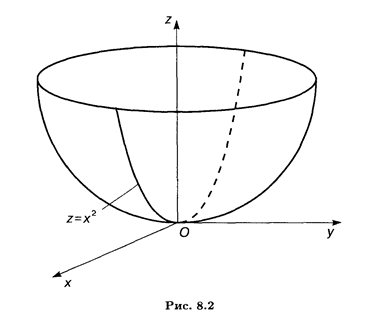


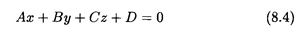
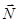 = (А, В, С) перпендикулярен плоскости (8.4); он называется нормальным вектором этой плоскости. Если известно, что плоскость проходит через некоторую точку M0(x0, y0, z0), то она может быть задана уравнением
= (А, В, С) перпендикулярен плоскости (8.4); он называется нормальным вектором этой плоскости. Если известно, что плоскость проходит через некоторую точку M0(x0, y0, z0), то она может быть задана уравнением
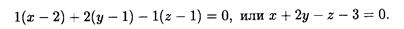
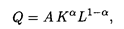

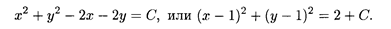
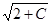 . Поверхность вращения (параболоид), описываемая данной функцией, становится "круче" по мере ее удаления от оси, которая дается уравнениями x = 1, у = 1.
. Поверхность вращения (параболоид), описываемая данной функцией, становится "круче" по мере ее удаления от оси, которая дается уравнениями x = 1, у = 1.