 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Применение в экономике
Рассмотрим два примера из экономики на использование числа е. Пример 1. Известно, что формула сложных процентов имеет вид
где Q0 — первоначальная сумма вклада в банк, р — процент начисления за определенный период времени (месяц, год), п — количество периодов времени хранения вклада, Q — сумма вклада по истечении п периодов времени. Формулы типа (2.4) используются также в демографических расчетах (прирост народонаселения) и в прогнозах экономики (увеличение валового национального продукта). Пусть первоначальный депозит Q0 помещен в банк под р = 100% годовых, тогда через год сумма депозита составит 2Q0. Предположим, что через полгода счет закроется с результатом
В общем случае, если р — процент начисления и год разбит на n частей, то через t лет сумма депозита достигнет величины
где r = р/100. Это выражение можно преобразовать:
Мы можем ввести новую переменную
Расчеты, выполненные по этой формуле, называют вычислениями по непрерывным процентам. Пример 2. Пусть темп инфляции составляет 1% в день.Насколько уменьшится первоначальная сумма через полгода? Решение. Применение формулы сложных процентов дает
где Q0 — первоначальная сумма, 182 — число дней в полугодии. Преобразуя это выражение, получаем
т.е. инфляция уменьшит первоначальную сумму примерно в 6 раз.
УПРАЖНЕНИЯ
Найти пределы следующих последовательностей. 2.1. 2.9. Прирост населения страны составляет р процентов в год. За сколько лет население страны удвоится? Дать ответ при а) р = 3% и б) р = 5%. 2.10. Коммерческий банк, обслуживающий предприятие по выдаче заработной платы, задерживает перечисляемые ему средства в среднем на 9 месяцев. За это время он успевает три раза "прокрутить" эти деньги в виде краткосрочных кредитов, выдаваемых частным предпринимателям на три месяца, под 3% в месяц. Сколько процентов прибыли получает банк на этой операции? 2.11. В условиях предыдущей задачи рассчитать, что выгоднее банку: кредитовать из собственных средств предприятия на условиях ставки годового процента, равной 20%, или заниматься вышеуказанной деятельностью. 2.12. Темп инфляции составляет 6% в месяц. Каков должен быть процент годовой ставки кредита, выдаваемого банком, чтобы прибыль от кредитования составляла 12% в год?
Глава 3. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ Понятие функции
Определение функциональной зависимости Определение 1. Пусть Х и Y — некоторые числовые множества и пусть каждому элементу x Кроме буквы f для обозначения функции используются и другие буквы, другими буквами может обозначаться также и независимая переменная. Примеры записи функций: у = у (x), y = F(x), y = g(x). Если множество Y значений функции ограничено, то функция называется ограниченной, в противном случае — неограниченной.
Способы задания функций
Задать функцию — значит указать закон, по которому, согласно определению, каждому значению аргумента из области определения ставится в соответствие (вычисляется) значение зависимой переменной из области значений функции. Существуют три основных способа задания функций: табличный, аналитический и графический. 1. Табличный способ. Этот способ имеет широкое применение в разных отраслях знаний и приложениях: ряды экспериментальных измерений, социологические опросы, таблицы бухгалтерской отчетности и банковской деятельности и т.п. Как правило, в таких таблицах по крайней мере одну из переменных можно принять за независимую (например, время), тогда другие величины будут являться функциями от этого аргумента. По сути дела базы данных основаны на табличном способе задания, хранения и обработки информации, а значит, и на табличной форме функциональной зависимости. 2. Аналитический способ. Этот способ состоит в задании связи между аргументом и функцией в виде формул. Следует подчеркнуть, что функция может определяться и набором формул — на разных промежутках области определения функции используются разные формулы. Приведем примеры аналитического задания функций. Пример 1. у = х3. Эта функция задана на бесконечной прямой -
Рис. 3.1 Пример 2. у =
Рис. 3.2
Пример 3. у = sign x = 0, если х = 0; -1, если х < 0. Термин sign происходит от латинского signum — знак. Функция задана на всем бесконечном промежутке (-
Рис. 3.3 Стрелки означают, что полупрямые не достигают точек ни оси ординат, так как при х = 0 значение функции определено по другому соответствию. 3. Графический способ. Здесь соответствие между аргументом и функцией задается посредством графика. Этот способ обычно используется в экспериментальных измерениях с употреблением самопишущих приборов (осциллографы, сейсмографы и т.п.).
Область определения функции
Остановимся на процедуре нахождения области определения функции. 1. В том случае, когда функция задана в аналитическом виде (посредством формулы)
и никаких ограничений или оговорок более не имеется, область ее определения устанавливается исходя из правил выполнения математических операций, входящих в формулу f в (3.1). Эти ограничения хорошо известны: подкоренное выражение в корне четной степени не может быть отрицательным, знаменатель дроби не может быть равным нулю, выражение под знаком логарифма должно быть только положительным, а также некоторые другие. Приведем здесь два примера. Пример 1.у = log2 (x2 — 5x + 6). Область определения этой функции находится из условия x2 — 5x + 6 > 0. Поскольку x = 2 и x = 3 — корни квадратного трехчлена, стоящего под знаком логарифма, то это условие выполняется на двух полубесконечных интервалах: (-
Рис. 3.4 Пример 2. у = arcsin Область определения этой функции находится из совокупности двух условий: аргумент под знаком arcsin не может быть по модулю больше единицы и знаменатель аргумента не должен равняться нулю, т.е.
Двойное неравенство эквивалентно двум более простым неравенствам: х + 2 ≥ 1 и х + 2 ≤ -1. Отсюда получаем, что область определения функции состоит из двух полубесконечных промежутков: (- 2. Область определения функции задана вместе с функцией f(x). Пример 3. у = 3x-4/3 + 2, 1 ≤ х ≤ 4.
3. Функция имеет определенный прикладной характер, и область ее существования определяется также и реальными значениями входящих параметров (например, задачи с физическим смыслом). Определение 2. Функция у = f(x) называется четной (симметрия относительно оси Оу), если для любых значений аргумента из области ее определения выполнено равенство
Определение 3. Функция у = f(x) называется нечетной (симметрия относительно начала координат О), если выполнено условие:
Например, функции у = х2 и у = cos x являются четными, а функции у = x3 и у = sin x— нечетными.
Приложения в экономике
Приведем примеры использования функций в области экономики. 1. Кривые спроса и предложения. Точка равновесия. Рассмотрим зависимости спроса D (demand) и предложения S (supply) от цены на товар Р (price). Чем меньше цена, тем больше спрос при постоянной покупательной способности населения. Обычно зависимость D от Р имеет вид ниспадающей кривой (рис. 3.5, а):
где а < 0. В свою очередь предложение растет с увеличением цены на товар, и потому зависимость S от Р имеет следующую характерную форму:
где b ≥ 1 (рис. 3.5, б). В формулах (3.2) и (3.3) с и d — так называемые экзогенные величины; они зависят от внешних причин (благосостояние общества, политическая обстановка и т.п.). Вполне понятно, что переменные, входящие в формулы (3.2) и (3.3), положительны, поэтому графики функций имеют смысл только в первой координатной четверти.
Рис. 3.5
Для экономики представляет интерес условие равновесия, т.е. когда спрос равен предложению; это условие дается уравнением
и соответствует точке пересечения кривых D и S — это так называемая точка равновесия (рис. 3.6). Цена Ро, при которой выполнено условие (3.4), называется равновесной.
Рис. 3.6
При увеличении благосостояния населения, что соответствует росту величины с в формуле (3.2), точка равновесия М смещается вправо, так как кривая D поднимается вверх; при этом цена на товар растет при неизменной кривой предложения S. 2. Паутинная модель рынка. Рассмотрим простейшую задачу поиска равновесной цены. Это одна из основных проблем рынка, означающая фактически торг между производителем и покупателем (рис. 3.7).
Рис. 3.7 Пусть сначала цену P1 называет производитель (в простейшей схеме он же и продавец). Цена P1 на самом деле выше равновесной (естественно, всякий производитель стремится получить максимум выгоды из своего производства). Покупатель оценивает спрос D1 при этой цене и определяет свою цену Р2, при которой этот спрос D1 равен предложению. Цена Р2 ниже равновесной (всякий покупатель стремится купить подешевле). В свою очередь производитель оценивает спрос D2, соответствующий цене P2, и определяет свою цену Р3, при которой спрос равен предложению; эта цена выше равновесной. Процесс торга продолжается и при определенных условиях приводит к устойчивому приближению к равновесной цене, т.е. к "скручиванию" спирали. Если рассматривать последовательность чисел, состоящую из называемых в процессе торга цен, то она имеет своим пределом равновесную цену Р0: Предел функции
Предел функции в точке
Пусть функция f(x) определена на некотором множестве X. Возьмем из Х последовательность точек
сходящуюся к точке а, причем а
и правомерно рассмотреть вопрос о ее сходимости. Определение. Число А называется пределом функции f(x) в точке а (или пределом функции при х Для обозначения предельного значения функции используется следующая символика: Приведем несколько примеров. Пример 1. Функция f(x) = С = const имеет предел в каждой точке числовой прямой. Действительно, любой последовательности (3.5), сходящейся к точке а, соответствует последовательность (3.6), состоящая из одного и того же числа C, откуда следует, что f(xn) Пример 2. Функция f(x) = х в любой точке а числовой прямой имеет предел, равный а. Действительно, последовательности значений аргумента (3.5) и значений функции (3.6) в этом случае тождественны, и если последовательность {xn} сходится к а, то и последовательность {f(xn)} также сходится к а. Пример 3. Функция f(x) =
Левый и правый пределы функции
Здесь вводятся и в дальнейшем будут использоваться понятия односторонних пределов функции: когда последовательность значений аргумента xn
Пример 4. Рассмотрим функцию f(x) = sign x (п. 3.1, пример 3). В точке x = 0 эта функция имеет левый и правый пределы:
Действительно, для любой сходящейся к нулю последовательности {xn}, у которой все элементы xп < 0 (xn > 0), соответствующая последовательность значений функции состоит только из одного числа -1 (+1), т.е. предел слева (справа) в точке x = 0 также равен этому числу. ТЕОРЕМА 1. Функция f(x) имеет в точке а предел тогда и только тогда, когда в этой точке существуют левый и правый пределы, причем они равны. В таком случае предел функции равен односторонним пределам.
Предел функции при х
Кроме понятия предела функции в точке существует также и понятие предела функции при стремлении аргумента к бесконечности. Для обозначения предела функции при x Приведем пример предела функции при х Аналогично можно доказать, что
Поиск по сайту: |
 (2.4)
(2.4)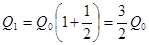 и эта сумма будет вновь помещена в качестве депозита в том же банке. В конце года депозит будет составлять
и эта сумма будет вновь помещена в качестве депозита в том же банке. В конце года депозит будет составлять  . Будем уменьшать срок размещения депозита в банке при условии его последующего размещения после изъятия. При ежеквартальном повторении этих операций депозит в конце года составит
. Будем уменьшать срок размещения депозита в банке при условии его последующего размещения после изъятия. При ежеквартальном повторении этих операций депозит в конце года составит 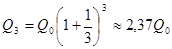 . Если повторять операцию изъятие-размещение в течение года сколько угодно раз, то при ежемесячном манипулировании сумма за год составит
. Если повторять операцию изъятие-размещение в течение года сколько угодно раз, то при ежемесячном манипулировании сумма за год составит  ; при ежедневном посещении банка
; при ежедневном посещении банка 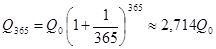 ; при ежечасном —
; при ежечасном —  и т.д. Нетрудно видеть, что последовательность значений возрастания первоначального вклада {qn} = {Qn/Q0} как раз совпадает с последовательностью, пределом которой является число ε при п
и т.д. Нетрудно видеть, что последовательность значений возрастания первоначального вклада {qn} = {Qn/Q0} как раз совпадает с последовательностью, пределом которой является число ε при п  согласно (2.4). Таким образом, доход, который можно получить при непрерывном начислении процентов, может составить за год не более чем
согласно (2.4). Таким образом, доход, который можно получить при непрерывном начислении процентов, может составить за год не более чем


 и при n
и при n 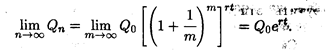
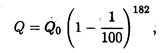
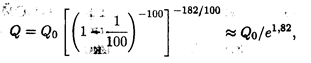
 2.2.
2.2.  2.3.
2.3.  2.4.
2.4.  2.5.
2.5. 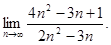 2.6.
2.6. 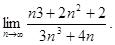 2.7.
2.7.  2.8.
2.8. 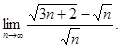
 Х по какому-либо закону f поставлен в соответствие один элемент у
Х по какому-либо закону f поставлен в соответствие один элемент у 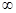 < x <
< x < 
 . Функция задана на отрезке [—1, 1], множество ее значений — отрезок [0, 1]. Это половина окружности, лежащая в верхней полуплоскости (рис. 3.2).
. Функция задана на отрезке [—1, 1], множество ее значений — отрезок [0, 1]. Это половина окружности, лежащая в верхней полуплоскости (рис. 3.2).
 +1, если x > 0;
+1, если x > 0;
 (3.1)
(3.1)
 .
.


 (3.2)
(3.2) (3.3)
(3.3)



 Pn = P0.
Pn = P0.
 X. Соответствующие значения функции в точках этой последовательности также образуют числовую последовательность
X. Соответствующие значения функции в точках этой последовательности также образуют числовую последовательность
 а), если для любой cходящейся к а последовательности (3.5) значений аргумента х, отличных от а, соответствующая последовательность значений функции (3.6) сходится к числу А.
а), если для любой cходящейся к а последовательности (3.5) значений аргумента х, отличных от а, соответствующая последовательность значений функции (3.6) сходится к числу А. f(x)
f(x)  имеет в точке x = 0 предел, равный -2. Действительно, пусть {xn} — любая последовательность значений аргумента, сходящаяся к нулю, т.е. lim xп = 0 при n
имеет в точке x = 0 предел, равный -2. Действительно, пусть {xn} — любая последовательность значений аргумента, сходящаяся к нулю, т.е. lim xп = 0 при n 
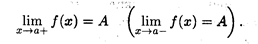


 f(x) = А.
f(x) = А.