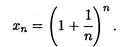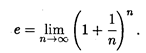|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Числовые последовательности и операции над ними
Числовые последовательности представляют собой бесконечные множества чисел. Примерами последовательностей могут служить: последовательность всех членов бесконечной геометрической прогрессии, последовательность приближенных значений Определение 1. Если каждому числу n из натурального ряда чисел 1, 2, 3,..., п,... поставлено в соответствие вещественное число xп, то множество вещественных чисел
x1, x2, x3, …, xn, … (2.1)
называется числовой последовательностью, или просто последовательностью. . Числа х1, x2, x3, ..., xп, ... будем называть элементами, или членами последовательности (2.1), символ xп — общим элементом, или членом последовательности, а число п — его номером. Сокращенно последовательность (2.1) будем обозначать символом {хп}. Например, символ {1/n} обозначает последовательность чисел
Иными словами, под последовательностью можно понимать бесконечное множество занумерованных элементов или множество пар чисел (п, xп), в которых первое число принимает последовательные значения 1, 2, 3, ... . Последовательность считается заданной, если указан способ получения любого ее элемента. Например, формула xп = -1 + (-1)n определяет последовательность 0, 2, 0, 2,... . Геометрически последовательность изображается на числовой оси в виде последовательности точек, координаты которых равны соответствующим членам последовательности. На рис. 2.1 изображена последовательность {хп} = {1/n} на числовой прямой.
Понятие сходящейся последовательности Определение 2. Число а называется пределом последовательности {xn}, если для любого положительного числа ε существует такой номер N, что при всех п > N выполняется неравенство
Последовательность, имеющая предел, называется сходящейся. Если последовательность имеет своим пределом число а, то это записывается так:
Последовательность, не имеющая предела, называется расходящейся. Определение 3. Последовательность, имеющая своим пределом число а = 0, называется бесконечно малой последовательностью. Замечание 1. Пусть последовательность {хп} имеет своим пределом число а. Тогда последовательность {αn}= {xn — a} есть бесконечно малая, т.е. любой элемент xп сходящейся последовательности, имеющей предел а, можно представить в виде
где αn — элемент бесконечно малой последовательности {αn}. Замечание 2. Неравенство (2.2) эквивалентно неравенствам (см. свойство 4 модуля числа из п. 1.5)
Это означает, что при п > N все элементы последовательности {xn} находятся в ε-окрестности точки а (рис. 2.2), причем номер N определяется по величине ε. Интересно дать геометрическую интерпретацию этого определения. Поскольку последовательность представляет собой бесконечное множество чисел, то если она сходится, в любой ε-окрестности точки а на числовой прямой находится бесконечное число точек — элементов этой последовательности, тогда как вне ε-окрестности остается конечное число элементов. Поэтому предел последовательности часто называют точкой сгущения. Замечание 3. Неограниченная последовательность не имеет конечного предела. Однако она может иметь бесконечный предел, что записывается в следующем виде:
Если при этом начиная с некоторого номера все члены последовательности положительны (отрицательны), то пишут
Если {xn} — бесконечно малая последовательность, то {1/xп} — бесконечно большая последовательность, имеющая бесконечный предел в смысле (2.3), и наоборот. Приведем примеры сходящихся и расходящихся последовательностей. Пример 1. Показать, используя определение предела последовательности, что Решение. Возьмем любое число ε > 0. Так как
то чтобы выполнялось неравенство (2.2), достаточно решить неравенство 1 / (n + 1) < ε, откуда получаем n > (1 — ε) / ε. Достаточно принять N = [(1 — ε)/ε] (целая часть числа (1 — ε)/ ε)* , чтобы неравенство |xп — 1| < ε выполнялосьпривсех п > N. * Символ [a] означает целую часть числа а, т.е. наибольшее целое число, не превосходящееа. Например,[2] = 2, [2,5] = 2, [0,8] = 0, [-0, 5] = -1, [-23,7] = -24. Пример 2. Показать, что последовательность {хп} = (-1)n, или -1, 1, -1, 1,... не имеет предела. Решение. Действительно, какое бы число мы ни предположили в качестве предела: 1 или —1, при ε < 0,5 неравенство (2.2), определяющее предел последовательности, не удовлетворяется — вне ε -окрестности этих чисел остается бесконечное число элементов xп: все элементы с нечетными номерами равны —1, элементы с четными номерами равны 1.
Основные свойства сходящихся последовательностей
Приведем основные свойства сходящихся последовательностей, которые в курсе высшей математики сформулированы в виде теорем.
1. Если все элементы бесконечно малой последовательности {хп} равны одному и тому же числу с, то с = 0. 2. Сходящаяся последовательность имеет только один предел. 3. Сходящаяся последовательность ограничена. 4. Сумма (разность) сходящихся последовательностей {хп} и {уп} есть сходящаяся последовательность, предел которой равен сумме (разности) пределов последовательностей {xп} и {yп}. 5. Произведение сходящихся последовательностей {хп} и {уп} есть сходящаяся последовательность, предел которой равен произведению пределов последовательностей {хп} и {уп}. 6. Частное двух сходящихся последовательностей {хп} и {уп} при условии, что предел последовательности {уп} отличен от нуля, есть сходящаяся последовательность, предел которой равен частному пределов последовательностей {хп} и {yп}. 7. Если элементы сходящейся последовательности {хn} удовлетворяют неравенству xп ≥ b (хп ≤ b) начиная с некоторого номера, то и предел а этой последовательности удовлетворяет неравенству а ≥ b (а ≤ b). 8. Произведение бесконечно малой последовательности на ограниченную последовательность или на число есть бесконечно малая последовательность. 9. Произведение конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
Рассмотрим применение этих свойств на примерах. Пример 3. Найти предел Решение. При n
Пример 4. Найти предел последовательности {xп} = Решение. Здесь, как и в предыдущем примере, числитель и знаменатель не имеют конечных пределов, и потому сначала необходимо выполнить соответствующие преобразования. Поделив числитель и знаменатель на n, получаем
Поскольку в числителе стоит произведение бесконечно малой последовательности на ограниченную последовательность,то в силу свойства 8 окончательно получаем
Пример 5. Найти предел последовательности {хп} = Решение. Здесь применить непосредственно теорему о пределе суммы (разности) последовательностей нельзя, так как не существует конечных пределов слагаемых в формуле для {хп}. Умножим и разделим формулу для {хn} на сопряженное выражение
Число е
Рассмотрим последовательность {хп}, общий член которой выражается формулой
В курсе математического анализа доказывается, что эта последовательность монотонно возрастает и имеет предел. Этот предел называют числом е. Следовательно, по определению
Число е играет большую роль в математике. Далее будет рассмотрен способ его вычисления с любой требуемой точностью. Отметим здесь, что число е является иррациональным; его приближенное значение равно е = 2,7182818... .
Поиск по сайту: |
 (x1 = 1, х2 = 1,4, х3 = 1,41, ...), последовательность периметров правильных n-угольников, вписанных в данную окружность. Уточним понятие числовой последовательности.
(x1 = 1, х2 = 1,4, х3 = 1,41, ...), последовательность периметров правильных n-угольников, вписанных в данную окружность. Уточним понятие числовой последовательности. .
.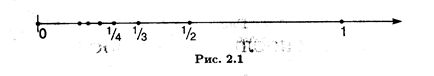
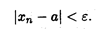 (2.2)
(2.2)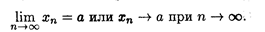
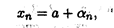
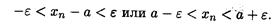
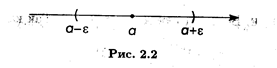
 (2.3)
(2.3)
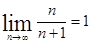 .
.
 .
. числитель и знаменатель дроби стремятся к бесконечности, т.е. применить сразу теорему о пределе частного нельзя, так как она предполагает существование конечных пределов последовательностей. Преобразуем данную последовательность, разделив числитель и знаменатель на n2. Применяя затем теоремы о пределе частного, пределе суммы и снова пределе частного, последовательно находим
числитель и знаменатель дроби стремятся к бесконечности, т.е. применить сразу теорему о пределе частного нельзя, так как она предполагает существование конечных пределов последовательностей. Преобразуем данную последовательность, разделив числитель и знаменатель на n2. Применяя затем теоремы о пределе частного, пределе суммы и снова пределе частного, последовательно находим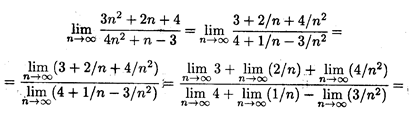
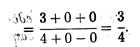
 при п
при п 

 при п
при п  :
: