 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Грани числовых множеств
Будем говорить, что множество Х ограничено сверху (снизу), если существует число d, такое, что для любого х Любое ограниченное сверху (снизу) множество имеет бесконечное число верхних (нижних) граней. Действительно, если число d является верхней гранью множества X, то и любое число d1 > d, согласно определению верхней грани, также будет верхней гранью этого множества. Наименьшая верхняя грань множества X, ограниченного сверху, называется точной верхней гранью этого множества; она обозначается символом supX. Наибольшая нижняя грань ограниченного снизу множества Х называется точной нижней гранью этого множества и обозначается символом infX. Эти символы заимствованы из латинского языка:supremum — наивысший иinfimum — наинизший. Приведем некоторые примеры. Пусть Х = (а, b). В таком cлучае числа а и b являются точными нижней и верхней гранями множества X, т.е. а = inf X, b = sup X. Пусть X = (- Известна следующая теорема о существовании точной верхней (нижней) грани числового множества, которую мы приводим ниже без доказательства. ТЕОРЕМА 1. Если непустое числовое множество ограничено сверху (снизу), то оно имеет точную верхнюю (нижнюю) грань. Абсолютная величина числа Приведем определение абсолютной величины вещественного числа х (модуля числа):
|x| = -х, если х < 0.
Из этого определения следует ряд свойств абсолютной величины, который мы приводим ниже без доказательств. 1. |х| ≥ 0. 2. |х| = | - x|. 3. -|х| ≤ х ≤ |x| . 4. Пусть а — положительное число. Тогда неравенства |х| ≤ а и -а ≤ х ≤ а равносильны. 5. Для любых двух действительных чисел х и у справедливо неравенство |x + y| ≤ |x| + |y|. В это свойство можно включить также и неравенство
|х – у| ≤ |х| + |у|.
6. Для любых двух действительных чисел х и y справедливо неравенство
|х – y| ≥ |х| -|у|. УПРАЖНЕНИЯ
Определить множества значений x, удовлетворяющих следующим условиям.
1.1.|х|<2.1.2. x2 ≤ 9.1.3. х2 > 25. 1.4. |x – 3| <1.1.5. (x2 + l) ≤ 17. 1.6 (x2 - 3)≥1.1.7. х - х2 > 0. 1.8. x2 – 2x + 7 > 0.1.9.x2 – 2x + 5 < 0.
Поиск по сайту: |
 Х выполняется неравенство х ≤ d (х ≥ d). Число d тогда называется верхней (нижней) гранью множества X. Множества, ограниченные снизу и сверху, называются ограниченными. Любой конечный промежуток ограничен. Интервалы (а, +
Х выполняется неравенство х ≤ d (х ≥ d). Число d тогда называется верхней (нижней) гранью множества X. Множества, ограниченные снизу и сверху, называются ограниченными. Любой конечный промежуток ограничен. Интервалы (а, + 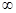 ) и (-
) и (-  х, если х ≥ 0;
х, если х ≥ 0;