 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
Дискретизация тела Метод конечных элементов (МКЭ) является современным средством приближённого решения различных задач математической физики, теории упругости, строительной механики. Метод конечных элементов, как и многие другие численные методы, основан на представлении реальной континуальной конструкции еедискретной модельюи замене дифференциальных уравнений, описывающих напряжённо-деформированное состояние сплошных тел, системой алгебраических уравнений.Вместе с тем МКЭ допускает ясную геометрическую, конструктивную и физическую интерпретацию. Рассмотрим упругое тело, нагруженное произвольным образом. Секущими плоскостями разобьём его на отдельные части, называемые конечными элементами (КЭ). На границах между конечными элементами наметим узлы, в которых элементы соединяются между собой. Если узлы находятся только в угловых точках КЭ, то такие КЭ называются конечными элементами первого порядка. Если есть дополнительные узлы посередине сторон КЭ, то получаются конечные элементы второго порядка (рис. 7.1).
Рис. 7.1. Дискретизация пластинки: а – пластинка;б – разбивка пластинки на конечные элементы;в – конечные элементы первого порядка;г – конечные элементы второго порядка
В дальнейшем будем считать перемещения этих узлов (линейные и угловые) основными неизвестными задачи и обозначать буквой Z. В зависимости от конкретного объекта число перемещений одного узла может меняться от одного до шести и называется степенью свободыузла. Число перемещений всех узлов КЭ называется степенью свободы КЭ. На рис. 7.2 показаны примеры конечных элементов и перемещения отдельного узлов для расчётов некоторыхобъектов. Важным этапом расчёта методом конечных элементов является выражение перемещений внутренних точек КЭ через перемещения узлов этого КЭ. Для этого используют локальные базисные (координатные) функции, аналогичныевыражениям(5.12), значения которых равны единице по направлению одной степени свободы и равны нулю по направлению всех остальных степеней свободы КЭ.Базисные функции должны удовлетворять следующим требованиям: · соответствовать главным граничным условиям задачи; · обеспечивать совместность деформаций внутри конечного элемента и на его границах с соседними элементами; · быть линейно независимыми; · обеспечивать перемещения КЭ как жёсткого целого и возможность постоянной деформации в пределах КЭ.
Рис. 7.2. Конечные элементы и узловые перемещения: а – для плоской задачи, б – для тонкой изгибаемой пластинки, в – для объёмной задачи
При выполнении указанных требований конечные элементы называются совместными конечными элементами, а с увеличением числа КЭ в дискретной схеме решение монотонно приближается к точному. Любые внешние поверхностные и объёмные нагрузки заменяют эквивалентнымив энергетическом смысле силами, приложенными в узлах. Задание приближённого поляперемещений внутри КЭ можно рассматривать как форму метода Ритца, а обобщённые перемещения – как перемещения узлов КЭ. Выражая потенциальную энергию деформации КЭ через узловые перемещения и минимизируя её, получают систему алгебраических уравнений относительно узловых перемещений КЭ.Это даёт возможностьсоставить матрицу жёсткости КЭ.Дальнейший расчётобъекта выполняется методами строительной механики. 7.2. Получение матрицы жёсткости
Выясним, обеспечат ли эти функции совместность конечного элемента. Поскольку координаты точек x и y стоят в первой степени, границы КЭ будут прямолинейными и совпадут с границами соседних элементов. Отличие от нуля коэффициентов Из этого следует, что принятое поле перемещений соответствует совместному конечному элементу. Формулы для перемещений запишем в матричной форме:
Введём вектор узловых перемещений Для его составления в формулу (7.1) подставим координаты узлов
Выразим из (7.2) вектор коэффициентов
Чтобы матрица L имела обратную, она должна быть квадратной. Поэтому число коэффициентов Подставим (7.3) в (7.1):
где матрица Деформации в произвольной точке найдём по уравнениям Коши (2.2)
где матрица Составим выражение для потенциальной энергии конечного элемента, используя формулу (5.5), при отсутствии поверхностных и объёмных сил:
Матрица упругих постоянных (2.18) при плоском напряжённом состоянии может быть записана в виде Формулу для потенциальной энергии деформации представим так:
Полученное выражение представляет собой квадратичную форму потенциальной энергии. Матрица
Эта матрица получена в местной системе координат КЭ, начто указывает штрих в её обозначении. Для КЭ толщиной t можно записать
гдеА – площадь КЭ. Выражение (7.9), хотя и составлено для плоского треугольного конечного элемента, однако оно носит общий характер. Матрицу жёсткости КЭ можно вычислить, зная упругие характеристики материала, входящие в матрицу Для рассмотренного треугольного КЭ матрица
где V – объём конечного элемента.
Поиск по сайту: |


 и
и  обеспечивает перемещения КЭ на плоскости как жёсткого целого. Выражения для относительных деформаций
обеспечивает перемещения КЭ на плоскости как жёсткого целого. Выражения для относительных деформаций 
 показывают возможность постоянной деформации внутри элемента.
показывают возможность постоянной деформации внутри элемента.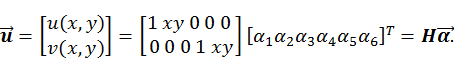 (7.1)
(7.1)
 (7.2)
(7.2) (i =1. . . 6) через узловые перемещения:
(i =1. . . 6) через узловые перемещения: (7.3)
(7.3) (7.4)
(7.4) называется матрицей базисных функций, с помощью которой перемещения любой точки КЭ выражаются через перемещения узловых точек. В матрице
называется матрицей базисных функций, с помощью которой перемещения любой точки КЭ выражаются через перемещения узловых точек. В матрице  , состоящей из двух строк и шести столбцов, будут элементы, содержащие переменные координаты x и y.
, состоящей из двух строк и шести столбцов, будут элементы, содержащие переменные координаты x и y. (7.5)
(7.5) (7.6)
(7.6)

 (7.7)
(7.7) (7.8)
(7.8)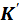 является матрицей жёсткости, которая соответствует вектору узловых перемещений
является матрицей жёсткости, которая соответствует вектору узловых перемещений 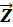 :
: . (7.9)
. (7.9) (7.10)
(7.10) и матрицу
и матрицу  (7.6), переводящую узловые перемещения в деформации КЭ.
(7.6), переводящую узловые перемещения в деформации КЭ. (7.11)
(7.11)