 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Простое и сложное нагружение. Разгрузка
Нагружение тела называется простым, если все компоненты тензора напряжений возрастают пропорционально одному параметру. В другом случае нагружение называется сложным. Иногда простым называют нагружение, при котором компоненты девиатора напряжений возрастают пропорционально одному параметру. Нагрузим тонкостенную трубку растягивающей силой и скручивающим моментом. В точках поперечного сечения возникнут нормальные и касательные напряжения, что приведёт к плоскому напряжённому состоянию. Если сила и момент будут увеличиваться пропорционально одному параметру, то нагружение будет простым. Если вначале трубку растянуть, а затем при неизменной силе скручивать, то нагружение будет сложным. При упругих деформациях последовательность нагружений (история нагружений) не имеет значения, необходимознать начальное и конечное (деформированное) состояния тела. При упругопластическом деформировании конечный результат зависит от истории приложения нагрузок. Возникает вопрос, как должны возрастать внешние силы, чтобы во всех точках тела при объёмном напряжённом состоянии нагружение было простым. Частичное решение этой задач было дано А.А. Ильюшиным в виде теоремы о простом нагружении: Чтобы во всех точках несжимаемого тела (µ = 0,5), нагруженного внешними силами, возрастающими пропорционально некоторому параметру β, нагружение было простым, достаточно, чтобы зависимость интенсивности напряженийот интенсивности деформаций была степенной функцией вида sи = Приближённо можно считать нагружение тела простым, если все внешние силы возрастают пропорционально одному и тому же параметру.
Закон разгрузки имеет вид sи = При полной разгрузке тела упругие деформации Пусть изгибающий момент М достигнет такой величины, при которой упругая зона поперечного сечения будет иметь размер 2∙h/6, а в остальной части поперечного сечения напряжения станут равны пределу текучести sТ (рис. 9.3). Если бы материал балки был идеально упругим, то напряжения распределялись бы по линейному закону:
Рис. 9.3. Остаточные напряжения после пластического изгиба балки
После снятия момента Мостаточные напряжения в балке будут равны: sост = s – s*
Поиск по сайту: |
 , (9.7)
, (9.7)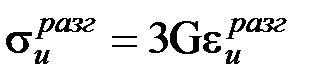 , (9.8)
, (9.8)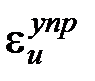 исчезают, а проявляются остаточные деформации
исчезают, а проявляются остаточные деформации  . Согласно теореме Генки, при разгрузке возникают остаточные напряжения, равные разности между истинными напряжениями в упруго-пластическом теле и теми напряжениями, которые создавались бы в нём в случае идеальной упругости материала.Например, если от точки А (рис. 9.2) полностью разгрузить тело, то остаточные напряжения
. Согласно теореме Генки, при разгрузке возникают остаточные напряжения, равные разности между истинными напряжениями в упруго-пластическом теле и теми напряжениями, которые создавались бы в нём в случае идеальной упругости материала.Например, если от точки А (рис. 9.2) полностью разгрузить тело, то остаточные напряжения  будут изображаться отрезком AD. Применим это свойство к чистому изгибу балки прямоугольного поперечного сечения, выполненной из идеального упругопластического материала (рис. 9.1, е).
будут изображаться отрезком AD. Применим это свойство к чистому изгибу балки прямоугольного поперечного сечения, выполненной из идеального упругопластического материала (рис. 9.1, е). с максимальной величиной:
с максимальной величиной: 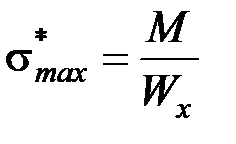 .
.
 Эпюра остаточных напряжений получается самоуравновешенной, т.е. в поперечном сечении нет изгибающего момента и продольной силы.
Эпюра остаточных напряжений получается самоуравновешенной, т.е. в поперечном сечении нет изгибающего момента и продольной силы.