 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Перемещения и деформации в точке тела
Все перемещения являются непрерывными функциями координат u = u(x,y,z); v=v(x,y,z);w = w(x,y,z). Деформации тела в точке представляют
Положительными считают деформации при растяжении, отрицательными – при сжатии. Изменение угла между гранями параллелепипеда называют углом сдвига, а соответствующую деформацию – сдвигом. Углы сдвига имеют следующие обозначения:
Рис. 1.13. Углы сдвига
Тензор деформаций По аналогии с тензором напряжений введено понятие «тензор деформаций»:
Тензор деформаций полностью описывает деформированное состояние в точке тела. В каждой точке тела можно найти три взаимно перпендикулярных направления, вдоль которых возникают только деформации растяжения или сжатия, а деформации сдвига отсутствуют. Такие осевые деформации называются главными деформациями ε1, ε2и ε3. Величины главных деформаций находят из решения кубического уравнения, аналогичному уравнению (1.2):
Инварианты тензора деформаций определяют по формулам:
Рассмотрим прямоугольный параллелепипед,грани которого параллельныглавным осям деформаций. Так как сдвиговые деформации отсутствуют, то объем деформированного элемента определяется произведением изменённых сторон деформированного элемента: – новый объём элемента:
– приращение объёма
– относительную объемную деформацию:
Таким образом, первый инвариант тензора деформаций определяет изменение объема в точке твердого деформированного тела. Как и тензор напряжений, тензор деформаций
Средняя деформация, которая характеризует объемную деформацию в точке:
Девиатордеформаций определяет изменение формы. Первый инвариант(изменение объема) девиатора деформаций равен нулю.Второй инвариантдевиатора деформаций определяется по формуле
Осевая деформация в направлении, перпендикулярном октаэдрической площадке, выражается через первый инвариант тензора деформаций:
а угол сдвига на октаэдрической площадке – через второй инвариант:
В теории пластичности используют понятие «интенсивность деформаций сдвига»
=
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ 1. На каких допущениях основана теория упругости? 2. В чем заключается принцип Сен-Венана? 3. Что называется напряжением? 4. Что называется тензоромнапряжений? 5. Какой смысл имеют индексы в обозначении касательного напряжения? 6. Какие напряжения и площадки называются главными? 7. Как вычислить первый инвариант тензора напряжений? 8. На какие составляющие раскладываются тензор напряжений? 9. Как вычислить наибольшие касательные напряжения? 10. Какие напряжения называются октаэдрическими и как они вычисляются? 11. Что называется тензором деформаций? 12. Какие деформации называются главными и как они обозначаются? 13. На какие составляющие раскладывается тензор деформаций? 14. Какой смысл имеет первый инвариант тензора деформаций и как его вычислить?
Поиск по сайту: |

 (рис. 1.13). Индексы указывают координатную плоскость, в которой происходит сдвиг. Положительный сдвиг соответствует уменьшению прямого угла между гранями параллелепипеда, отрицательный – увеличению угла. Согласно обозначениям
(рис. 1.13). Индексы указывают координатную плоскость, в которой происходит сдвиг. Положительный сдвиг соответствует уменьшению прямого угла между гранями параллелепипеда, отрицательный – увеличению угла. Согласно обозначениям  ,
,  ,
,  .
. .
.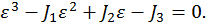 (1.3)
(1.3)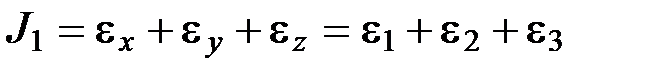 ;
; ;
;
 .
. ,
,  ,
,  . Пренебрегая произведениями относительных деформаций, вычислим:
. Пренебрегая произведениями относительных деформаций, вычислим: ;
;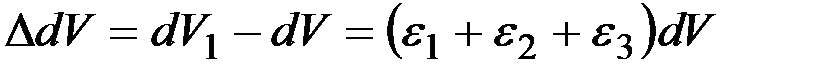 ;
; .
. можно представить в виде суммы шарового тензора деформаций и девиатора деформаций:
можно представить в виде суммы шарового тензора деформаций и девиатора деформаций: ;
;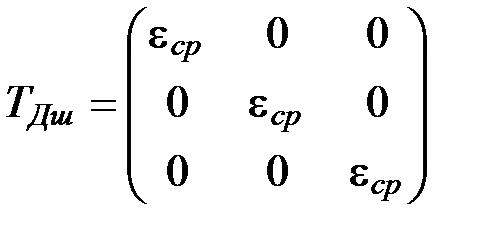 ;
; .
. .
. .
.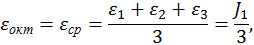
 .
. :
: =
=