 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Функционал полной энергии деформированного тела.
Для твёрдого деформируемого тела вводится понятие полной энергии Э, равной сумме потенциальной энергии деформациитела (потенциалу внутренних сил) U и энергии внешних сил(потенциалу внешних сил) Т: Э=U+Т. (5.2) В недеформированном состоянии Э=Э0=0. Поэтому энергия Э равна изменению энергии внешних и внутренних сил при переходе из начального состояния в деформированное. Энергия тела численно равна работе, которую совершают указанные силы при переводе системы из деформированного состояния в начальное состояние, для которого Э0=0. Из курса «Сопротивление материалов» известно, что удельная потенциальная энергия деформации, накапливаемая в единице объёма материала при растяжении, вычисляется по формуле U0=0,5σε. Обобщив эту формулу на случай объёмного напряжённого состояния, получаем
Для всего объёма тела V потенциал внутренних сил находим интегрированием:
где векторы напряжений
По аналогии определим работу объёмных сил, действующих на бесконечно малый объём dV:
Полный потенциал получим интегрированием по поверхности тела S и объёму V:
Используя матричные выражения (2.9), можно записать:
Формулудля
Теперь выражение для полной энергии принимает вид:
Полную энергию деформированного тела можно рассматривать как функционал, зависящий от функций, определяющих перемещения точек тела Напомним, что в формуле (5.5) 5.3. Вариационный принцип Лагранжа Согласно принципу возможных перемещений Лагранжа для системы, находящейся в равновесии, сумма работ всех внешних и внутренних сил на произвольных малых перемещениях, которые допускаются связями системы, равна нулю. Пусть возможные малые перемещения
Разложим выражение для
Здесь При бесконечно малых значениях Тогда получаем
Следовательно, функционал полной энергии тела (5.5) при условии (5.7) становится стационарным, т.е. принимает экстремальное значение. Дополнительный анализ показывает, что вторая вариация функционала Из равенства (5.7) следует, что из всех возможных перемещений действительными, обеспечивающими равновесие тела при заданных внешних нагрузках, будут те перемещения, при которых функционал Условие (5.7) называется вариационным уравнением Лагранжа.
Поиск по сайту: |
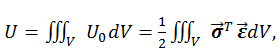(5.3)
и деформаций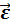 
определены формулами (2.9).
(5.4)
преобразуем, используя выражения (2.21):
(5.5)
– матрица жёсткости (матрица упругих характеристик материала), вычисляемая по выражению (2.18), 
–матрица дифференцирования (2.11).
заданы как вариации функций 
. Это приводит к изменению полной энергии тела на величину 
, которую можно выразить как сумму приращенийпотенциалов внешних сил 
и внутренних сил 
. Поскольку эта сумма численно равна работе внешних и внутренних сил на возможных перемещениях, т.е. нулю, то
(5.6)
( 
( 
– первая вариация функционала полной энергии, линейно зависящая от вариации перемещений 
; 
( 
Э –вторая вариация функционала полной энергии и т.д.
, как величинами более высокого порядка малости.
(5.7)
оказывается положительной, поэтому функционал (5.5) имеет минимальное значение.
(5.5) принимает стационарное значение.