 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ОСНОВЫ ТЕОРИИ ПЛАСТИЧНОСТИ
Основные определения Теория пластичности представляет собой раздел механики деформируемого твёрдого тела, в котором рассматриваются напряжения, деформации и перемещения, возникающие в пластически деформируемых телах. При малых деформациях строительные материалы подчиняются закону Гука. При появлении в растянутом образце напряжений, превышающих предел пропорциональности материала, зависимость между напряжениями s и относительной деформациейe становится нелинейной (рис. 9.1, а). Произвольной точкеВ на диаграмме напряжений соответствует упругая деформацияey и остаточная (пластическая) деформацияeост. Материал с подобной диаграммой деформирования называется упругопластическим. В расчётах за пределами упругости диаграммы напряжений схематизируют, заменяя отдельные участки прямыми или кривыми линиями с простым математическим выражением. Для материалов с явно выраженной площадкой текучести используют схему с линейным упрочнением (рис. 9.1, б) или со степенным упрочнением (рис. 9.1, в). Диаграмма напряжений без площадки текучести заменяется двумя прямыми (рис. 9.1, г) при линейном упрочнении или прямой и параболой (рис. 9.1, д) при степенном упрочнении. Для идеального упругопластического материала диаграмма принимается с неограниченной площадкой текучести (рис. 9.1, е), а в случае, когда упругими деформациями можно пренебречь, рассматриваютжесткопластический материал (рис. 9.1, ж).
Рис. 9.1. Схематизация диаграммы напряжений при растяжении стержня
Если для упругого материала при известной деформации можно однозначно определить величину нагрузки, то для упруго-пластичного материаладля определения нагрузки по известной деформации необходимо знать всю историю нагружения. В теории пластичности используются многие уравнения из линейнойтеории упругости: уравнения равновесия, геометрические уравнения, уравнения совместности деформаций. А вместо физических уравнений (законы Гука) используются другие зависимости. Напомним некоторые сведения из теории упругости. Напряжённое состояние материала в точке определяется тензором напряжений
который раскладывается на шаровой тензор напряжений
где
Существуют три инварианта тензораТs, которые вычисляются через элементы тензора (см. разд. 1) и через главные напряжения записываются так:
I1(Тs) = s1 + s2 + s3; I2(Тs) = s1s2 + s2s3 + s3s1; I3(Тs) = s1s2s3. В теории пластичности применяют такие понятия: «интенсивность касательных напряжений
где В случае чистого сдвига (s1= t, s2= 0, s3= –t) получаемtи = t. Деформированное состояние материала в точке описывается тензором деформаций:
Тензор деформаций
где ДевиатордеформацийDДопределяет изменение формы. Первый инвариант(изменение объема) девиатора деформаций равен нулю.Второй инвариантдевиатора деформаций определяется по формуле
В теории пластичности используют понятие «интенсивность деформаций сдвигаgи»:
и «интенсивность линейных деформаций» или просто «интенсивность деформаций»
В случае чистого сдвига Шаровые тензоры напряжений и деформаций связаны зависимостью
где К = Е/(3(1 – 2m)) – объёмныймодуль упругости. Девиаторы напряжений и деформацииподчиняются условию
В пределах упругости интенсивность нормальныхнапряжений прямо пропорциональна интенсивности деформаций:
9.2. Условия пластичности Из курса сопротивления материалов известно: 1) в случае осевого растяжения пластические деформации появляются, когда нормальные напряжения в поперечном сечении стержня достигают предела текучести: s = s1 = sт; 2) при кручении стержня круглого поперечного сечения возникает чистый сдвиг и пластические деформации появляются тогда, когда наибольшие касательные напряжения достигают предела текучести при сдвиге
Для объёмного напряжённого состояния условие текучести впервые было получено на основании опытов по истечению металлов через отверстия, проведённых в 1868 году французом Треска. Им было установлено, что в состоянии текучести наибольшие касательные напряжения во всех точках среды одинаковы и равны пределу текучести материала при чистом сдвиге. Математическую формулировку этого факта для плоского напряжённого состояниядалСен-Венан: s1 – s3 = sт, (9.5) а Леви распространил её на объёмное напряжённое состояние. Условие пластичности (9.5) называютусловиемТреска–Сен-Венана, а в курсе сопротивления материалов оно известно как теория прочности наибольших касательных напряжений. В формуле (9.5) не учитывается промежуточное главное напряжение s2 Многочисленные опыты показали, что при всестороннем растяжении или сжатии материал деформируется упруго, поэтому первый инвариант девиатора напряжений равен нулю и условие пластичности зависит от второго и третьего инвариантов девиатора напряжений. Губер и Мизес, исходя из разных предпосылок, предложили условие пластичности в виде sи = т.е. пластические деформации появляются тогда, когда интенсивность напряжений становится равной пределу текучести материала при растяжении. Указанное условие в сопротивлении материалов известно как энергетическая теория прочности. При чистом сдвиге (s1 = t, s2 = 0, s3 = –t) из условия (9.5) получаем
а из условия (9.6)
Опытами установлено, что пластические деформации при чистом сдвиге возникают тогда, когда
Поиск по сайту: |

 и девиатор напряжений
и девиатор напряжений 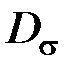 :
: ,
,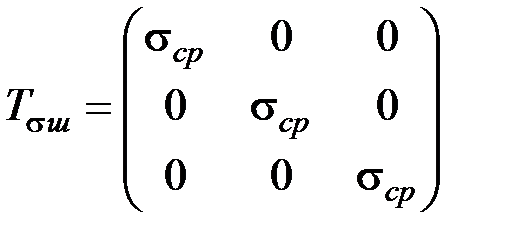 ,
,  ,
, .
. » и «интенсивность нормальных напряжений sи», которые формально выражаются черезI2(Ds):
» и «интенсивность нормальных напряжений sи», которые формально выражаются черезI2(Ds): ,
,
 .
. , как и тензор напряжений, можно представить в виде суммы шарового тензора деформаций и девиатора деформаций:
, как и тензор напряжений, можно представить в виде суммы шарового тензора деформаций и девиатора деформаций: ;
; ;
; .
.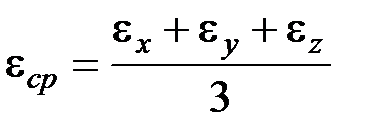 – средняя деформация, которая характеризует объемную деформацию в точке.
– средняя деформация, которая характеризует объемную деформацию в точке.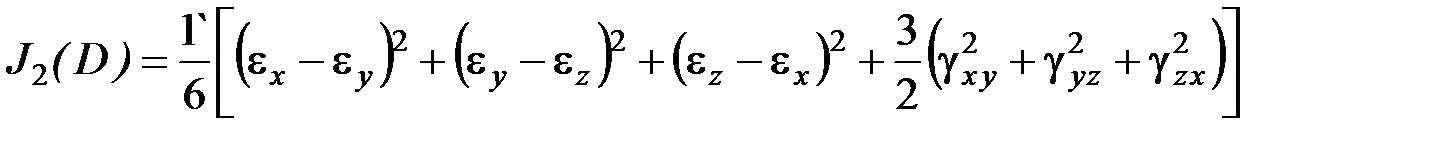 .
.
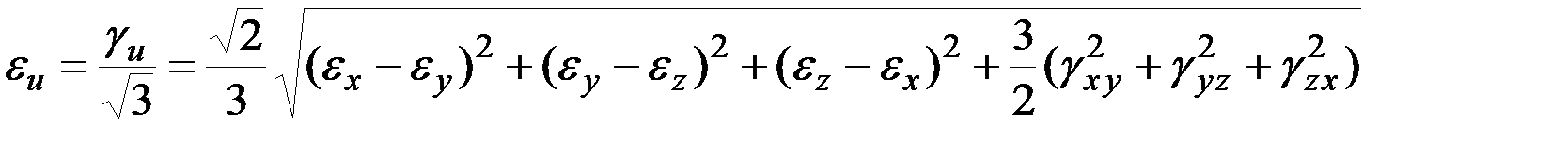 . (9.1)
. (9.1)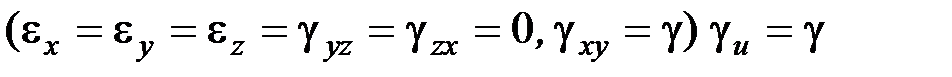 .
.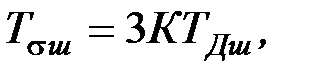 (9.2)
(9.2) (9.3)
(9.3) (9.4)
(9.4)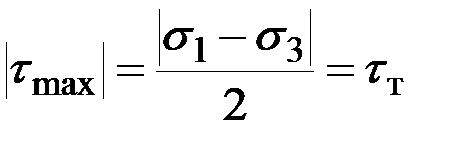 .
. что является недостатком условия Треска–Сен-Венана.
что является недостатком условия Треска–Сен-Венана. , (9.6)
, (9.6) ,
,
 ,т.е. условие (9.6) оказывается более точным. В практических расчётах применяют оба условия пластичности.
,т.е. условие (9.6) оказывается более точным. В практических расчётах применяют оба условия пластичности.