 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Теория пластического течения
Теорияпластического течения устанавливает связь между напряжениями и бесконечно малыми приращениями пластических деформаций Вводится понятие «интенсивность приращений пластических деформаций», выражение для которой аналогично выражению (9.1):
В теории используются три гипотезы. 1. Среднее нормальное напряжение прямо пропорционально объёмной деформации, при этом коэффициент пропорциональности тотже, что и в пределах упругости. Эта гипотеза совпадает с первой гипотезой теории малых упругопластических деформаций. Продифференцировав выражение (9.9), получаем
Приращение средней линейной деформации
Упругая часть приращения подчиняется закону Гука:
C учётом этого
2. Компоненты девиатора приращений пластических деформаций
В развёрнутой форме это условие имеет вид:
По аналогии с параметромy в теории малых упругопластических деформаций получается выражение дляdl:
3. Интенсивность напряжений является функцией интеграла от интенсивности приращений пластических деформаций, не зависящей от типа напряжённого состояния:
где Определим функцию Следовательно,
 . Поэтому для получения графика функции  необходимо построить график зависимости напряжения от пластической деформации. Пусть известна диаграмма растяжения материалаs = f(e) (рис. 9.4). Для произвольной точки В из полной деформации удалим упругую частьeу  сдвинув точку В по горизонтали в положение С. Выполнив подобные действия для всех точек кривой, расположенной выше точки А, получим искомую кривую:  .
Уравнения теории текучести значительно сложнее уравнений теории малых упругопластических деформаций. Доказано, что в случаях простого нагружения обе теории дают одинаковые результаты. Многочисленные опыты показали, что при сложном нагружении теория пластического течения даёт более достоверные результаты.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ 1. Какой материал называют упругопластическим? 2. Как вычисляется интенсивность касательных напряженийtи? 3. Как вычисляется интенсивность нормальных напряженийsи? 4. Как вычисляется интенсивность деформацийeи? 5. Как вычисляется интенсивность деформаций сдвигаgи? 6. Как записывается условие пластичности Треска–Сен-Венана? 7. Как записывается условие пластичности Губера-Мизеса? 8. Какое нагружение тела называется простым? 9. В чем заключается теорема о простом нагружении? 10. На каких гипотезах основана теория малых упругопластических деформаций? 11. На каких гипотезах основана теория пластического течения?
Поиск по сайту: |
. (9.11)
, (9.12)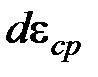
складывается из упругой части 
и пластической части 
:
.
.
= 0, т.е. за счёт пластических деформаций объём не изменяется. Поэтому тензор приращений пластических деформаций представляет собой девиатор
прямо пропорциональныкомпонентам девиатора напряженийDs:
.
(9.13)
.
, (9.14)
– интенсивность приращений пластических деформаций, определяемая по формуле (9.11).
(материал несжимаемый). Тогдаsи = s, 
.
.