 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Понятие о некоторых линиях в плоской задаче
Получив выражения для напряжений вплоской задаче как функции двух координат x,y, можно наложить на эти функции некоторые условия и тем самым найти уравнения некоторых линий. Такие линии дают наглядное представление о поле напряжений, позволяя визуально оценивать некоторые параметры напряжённого состояния. При анализе поля напряжений используют следующиелинии: изобары– линии, соединяющие между собой точки с одинаковыми главными нормальными напряжениями; изохромы– линии, соединяющие между собой точки с одинаковыми главными касательными напряжениями; изостаты(траектории главных напряжений) – линии, касательные к которым определяют направления главных нормальных напряжений; изоклины– линии, соединяющие между собой точки с одинаковым наклоном главных нормальных напряжений. 4.6. Примеры решения плоской задачи в полиномах
Начнём с полинома второго порядка:
Эта функция удовлетворяет бигармоническому уравнению (4.15) при любых коэффициентах С. Согласно уравнениям (4.13) получаем:
Первое слагаемое в формуле (4.16) соответствует осевой деформации в направлении оси y, второе слагаемое – деформации чистого сдвига, третье слагаемое – осевой деформации в направлении оси x (рис. 4.4).
Рис. 4.4. Напряжения на кромках пластинки На гранях пластинки поверхностная нагрузка совпадает со значениями напряжений. Полином третьего порядка
удовлетворяет бигармоническому уравнению (4.15) при любых коэффициентах С. Согласно уравнениям (4.13) получаем:
(4.19)
 . Остаются только нормальные напряжения . Остаются только нормальные напряжения 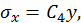 распределение которых показано на рис. 4.5. Совокупности поверхностных нагрузок налевой и правойкромках пластинкиобразуют изгибающие моменты Мz, поэтому пластинка испытывает деформацию плоского изгиба. распределение которых показано на рис. 4.5. Совокупности поверхностных нагрузок налевой и правойкромках пластинкиобразуют изгибающие моменты Мz, поэтому пластинка испытывает деформацию плоского изгиба.
Рассматривая последовательно ненулевые значения других коэффициентов С, получим набор различных поверхностных нагрузок и соответствующие им распределения напряжений внутри пластинки. Если порядок полинома выше третьего, то уравнение совместности деформаций (4.15) будет выполняться только при некоторых соотношениях между коэффициентамиполинома, вытекающих из этого уравнения. Имея набор решений отдельных задач, можно, комбинируя эти решения, анализировать напряжённое состояние для сложных случаев нагружения пластинки. Рассмотрим консольную треугольную пластинку единичной толщины, нагруженную линейно изменяющейся нагрузкой Используем выражения для функции напряжений и напряжений по формулам (4.18) и (4.19). Постоянные С1 . . . С4 определяем из граничных условий в точках А и В. В точке А(x; 0):
В точке В(
Согласно формулам (4.2) при отсутствии нагрузок на нижней грани
Из второго уравнения получаем Окончательно формулы для напряжений получают следующий вид:
Эпюры напряжений в сечении АВ пластинки приведены на рис. 4.6. Сопоставим полученные эпюрыс результатами расчёта по формулам сопротивления материалов. Нормальные напряжения σy в сопротивлении материалов вообще не вычисляют. Напряжения σx в крайних точках сечения АВ:
Это выражение полностью совпадает с результатом, полученным в теории упругости. Эпюра касательных напряжений, вычисляемых по формуле Журавского, изображается параболой (пунктир на рис. 4.6) с максимальной ординатой:
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ 1. Как записываются уравнения равновесия для плоской задачи теории упругости? 2. Как записываются геометрические уравнения для плоской задачи теории упругости? 3. Как записываются уравнения совместности деформаций для плоской задачи теории упругости? 4. Как записываются физические уравнения для плоской задачи теории упругости? 5. Как записывается уравнение совместности деформаций для плоской задачи теории упругости в напряжениях? 6. Как записывается бигармоническое уравнение для плоской задачи теории упругости? 7. Как выражаются напряжения через функцию напряжений? 8. Какой вид имеет функция напряжений, соответствующая осевой деформации в направлении оси х? 9. Какой вид имеет функция напряжений, соответствующая осевой деформации в направлении оси у? 10. Какой вид имеет функция напряжений, соответствующая чистому сдвигу? 11. Какой вид имеет функция напряжений, соответствующая чистому изгибу? 5. ВАРИАЦИОННАЯ ФОРМУЛИРОВКА ЗАДАЧ 5.1. Понятие о функционале Функционалом называется скалярная величина, зависящая от функций
Область определения Ω может быть одно-, двух- или трёхмерной. Функция Функция Например, функционалом является длина L кривой
Пусть имеются две функции одного класса При варьировании функции При некоторых условиях функционал обладает свойством стационарности (локальной экстремальности): произвольные бесконечно малые изменения функции-аргумента Такие функции, при которых функционал стационарен (имеет экстремум), называются экстремалями функционала. Задачи нахождения экстремалей (вариационные задачи) рассматриваются разделом математики, называемым вариационным исчислением. Известно, что необходимым условием стационарностифункционала является равенство нулю вариации функционала:
Вариационная задача является обобщением задачи о нахождении экстремума функции нескольких переменных. Если в обычной экстремальной задаче условие экстремума описывается системой конечного числа алгебраических или трансцендентных уравнений, то в вариационной задаче появляются дифференциальные уравнения (уравнения Эйлера), которые соответствуютконкретному функционалу. В теории упругости широко используются так называемые прямые методы решения вариационных задач, которые не сводят задачу к дифференциальным уравнениям.
Поиск по сайту: |
 (4.16)
(4.16) (4.17)
(4.17)



 (4.18)
(4.18)

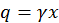 (рис. 4.6).
(рис. 4.6). 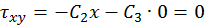 , откуда
, откуда  .
. , откуда
, откуда 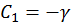 .
.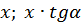 ):
): 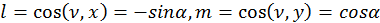 .
.
 , а после подстановки этого равенства в первое уравнение находим
, а после подстановки этого равенства в первое уравнение находим  .
. (4.20)
(4.20)

 , принадлежащих некоторому классу (множеству). Обычно функционал представляет собой определённый интеграл вида
, принадлежащих некоторому классу (множеству). Обычно функционал представляет собой определённый интеграл вида . (5.1)
. (5.1) рассматривается как аргумент функционала F, онадолжна быть непрерывной и дифференцируемой.
рассматривается как аргумент функционала F, онадолжна быть непрерывной и дифференцируемой. может зависеть не только от
может зависеть не только от 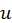 , но и от её частных производных.
, но и от её частных производных. , соединяющей на плоскости две точки:
, соединяющей на плоскости две точки:
 и
и  , отличающиеся при фиксированном аргументе
, отличающиеся при фиксированном аргументе  на бесконечно малую величину. Разность
на бесконечно малую величину. Разность  называется вариацией функции
называется вариацией функции  Вариация отличается от дифференциала функции
Вариация отличается от дифференциала функции  , т.е. от её приращения, вызванного изменением аргумента
, т.е. от её приращения, вызванного изменением аргумента  . Главная линейная часть приращения функционала называется вариацией функционала и обозначается
. Главная линейная часть приращения функционала называется вариацией функционала и обозначается  .
. (5.2)
(5.2)