 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Плоское напряжённое состояние и плоская деформация
Рассмотримпластинку малой толщины t, нагруженную некоторой нагрузкой, которая равномерно распределена по толщине пластинки (рис. 4.1). Выделим бесконечно малый элемент размерами dx, dy, t. На гранях элемента, совпадающими с наружными поверхностями пластинки, напряжения отсутствуют:
Рис. 4.1. Плоское напряжённое состояние
Пусть вытянутое в одном направлении тело ( Такой случай называется плоской деформацией. Выделим из пластинки бесконечно малый элемент, на гранях которого действуют показанные напряжения (рис. 4.2). Перемещения точек элемента направлены только вдоль осей x и y (w=0) и не зависят от координаты z. Поэтому в соответствии с формулой (2.2) Поскольку Рис. 4.2. Плоская деформация
4.2. Основные уравнения плоской задачи. Перепишем основные уравнения теории упругости применительно к плоскому напряжённому состоянию, исключив из них производные по z. Уравнения равновесия
Уравнения равновесия на поверхности тела
Геометрические уравнения
Уравнение совместности деформаций
Закон Гукав прямой форме
Закон Гука в обратной форме
В случае плоской деформации из всех полученных уравнений изменятся только формулы закона Гука из-за наличия напряжения
Поэтому для плоской деформации физические уравнения (закон Гука) будут отличаться от аналогичных уравнений плоского напряжённого состояния заменой
Плоское напряжённое состояние и плоская деформация рассматриваются как одна задача – плоская задача теории упругости.
Поиск по сайту: |
Вследствие малости размера t предполагаем, что такие напряжения равны нулю во всех точках пластинки. Такой вид напряжённого состояния называется плоским напряжённым состоянием. Линейные деформации возникают вдоль всех трёх координатных осей, причём из условия 
по закону Гука (2.6) получается
находится под действиемравномерно распределённой нагрузки (рис. 4.2), а торцы этого тела не перемещаются вдоль оси z. Вырежем пластинку толщиной 
в средней части тела. В отличие от случая плоского напряжённого состояния эта пластинка не изменяет своего размера в направлении оси z, так как этому препятствуют массивные части тела слева и справа от пластинки. Пластинка как бы зажата между абсолютно жёсткими телами.
и по закону Гука (2.7) 
, то по формуле (2.6) получаем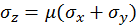 
.
(4.1)
(4.2)
(4.3)
(4.4)
(4.5)
(4.6)
. Если в первое уравнение системы (2.6) подставить 
то после преобразований получим
и 
на условные модуль упругости E1и коэффициент Пуассонаμ1:
; (4.7)
(4.8)