 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Геометрическиеуравнения
Геометрические уравнения устанавливают зависимости между деформациями и перемещениями. Рассмотрим проекцию бесконечно малогоэлемента на координатную плоскость
Рис. 2.2. Деформация прямоугольного элемента
На рис. 2.2 пунктиром показано деформированное положение элемента. Сторона АС удлинилась на величину, равную произведению градиента (интенсивности изменения) Аналогично определяется новое положение точки В (В1). Относительная деформация в направлении оси
Относительная деформация в направлении оси
Углы наклонов граней элемента:
Угол сдвига в плоскости
Для получения формул, выражающих другие деформации, можно
Уравнения Коши (2.2) связывают дифференциальными зависимостями шесть функций тензора деформаций с тремя функциями перемещений. Эти соотношения позволяют однозначно определить относительные линейные и сдвиговые деформации при произвольных непрерывных функциях перемещений. Решение же обратнойзадачи по определению трех функций перемещений из шести дифференциальных уравнений (2.2) при заданных деформациях получается неоднозначным. Система уравнений является переопределенной. При произвольно заданных шести компонентах деформаций три функции перемещений могут быть определены интегрированием любых трех соотношений Коши. При этом может оказаться, что три оставшихся уравнения не будут удовлетворяться. Поэтому компоненты тензора деформаций не могут назначаться произвольно. Между ними должны существовать определенные зависимости. Представим в плоскостихутвердое деформированное тело,разбитое на малые прямоугольные элементы (рис. 2.3,а). После деформаций элементы изменяют размеры и форму (рис. 2.3, б). Между соседними элементами не должно быть зазоров, разрывов. Деформации, удовлетворяющие этому условию, называются совместными деформациями. Соотношения между совместными деформациями называются уравнениями совместности деформаций. Чтобы получить условия совместности, исключим из уравнений Коши (2.2) функции перемещений. Для этого, продифференцировав первое и второе соотношения дважды поуихсоответственно и просуммировав результаты, получим
Рис. 2.3. Совместность деформаций Используя три последних уравнения системы (2.2), определим сумму Продифференцировав обе части этого равенства по x, получаем
Используя круговую подстановку обозначений, составляем на основе выражений (2.3) и (2.4) следующую систему уравнений совместности деформаций (уравнения Сен- Венана):
Первые три уравнения связывают линейные и угловые деформации в каждой координатной плоскости, а последние три уравнения связывают каждую линейную деформацию сугловыми деформациями во всех координатных плоскостях. Уравнения Коши (2.2) и уравнения Сен-Венана (2.5) образуют группу геометрических уравнений теории упругости. Физические уравнения Физические уравнения устанавливают связи между напряжениями и относительными деформациями, известные из курса «Сопротивление материалов» в виде обобщённого закона Гука:
Здесь E и G – модули упругости при растяжении и при сдвиге, µ – коэффициент Пуассона. Для изотропного материала эти характеристики материала связаны зависимостью
Уравнения (2.6) называют прямой формой закона Гука. Выражения напряжений через деформации называют обратной формой закона Гука:
Здесь
Поиск по сайту: |
 (рис. 2.2).
(рис. 2.2).
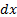





 перемещенияна длину элемента
перемещенияна длину элемента  , и наклонилась на угол
, и наклонилась на угол  перемещенияна длину элемента
перемещенияна длину элемента  :
:
 :
:
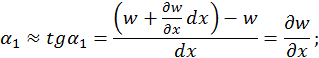



 После этого получаем следующие уравнения (уравнения Коши):
После этого получаем следующие уравнения (уравнения Коши): (2.2)
(2.2) . (2.3)
. (2.3) , которая будет равна
, которая будет равна 
 (2.4)
(2.4)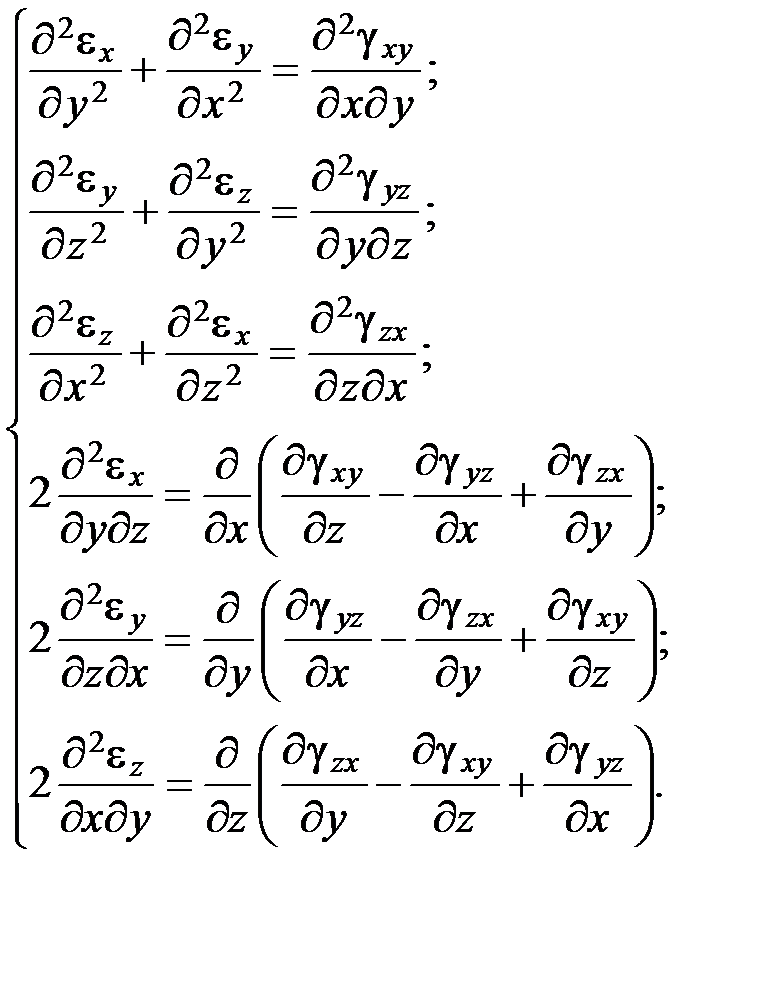 (2.5)
(2.5) (2.6)
(2.6) .
. (2.7)
(2.7) – относительное изменение объёма,
– относительное изменение объёма, –постояннаяЛаме. (2.8)
–постояннаяЛаме. (2.8)