 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Решение плоской задачи в напряжениях и перемещениях
Принимаем за основные неизвестные три напряженияsх = sх(х, y);
В уравнение совместности деформаций (4.4) подставим вместо деформаций их выражения через напряжения по (4.5)и вторуюпроизводную от касательных напряжений по (4.9). В результате получим
Поскольку
Условие (4.10) выражает уравнение совместности деформаций, записанное через напряжения, и называется уравнением Леви. Таким образом, решение плоской задачи в напряжениях основывается на системе трёх уравнений
По-прежнему, условия на контуре пластинки (граничные условия) определяются формулами (4.2). Поскольку выражения (4.11) не включают упругие постоянные материалаЕ и μ, то полученные с их помощью решения пригодны для пластинок, выполненных из любого изотропного материала. Примем теперь основными неизвестными перемещения В результате после преобразований получим следующие уравнения плоской задачи в перемещениях:
Граничные условия на контуре пластинки (4.2) следует записать, выразив напряжения
Функция напряжений Решение плоской задачи в напряжениях при постоянных объёмных силах
Эта функция называется функцией напряжений или функцией Эйри. Подстановка формул напряжений (4.13) в первые два уравнения (4.11) превращает эти уравнения в тождества. Подставив формулы (4.13) в третье уравнение системы (4.11), получим
Оператор В развёрнутом виде формула (4.14) имеет вид
Уравнение (4.15) называется бигармоническим уравнением плоской задачи. Оно выражает условиесовместности деформаций, выраженное через функцию напряженийφ. Следовательно, для решения плоской задачи в напряжениях необходимо отыскать только одну неизвестную функцию координат – функцию напряжений φ(x,y), удовлетворяющую условиям на контуре пластинки. Сами напряжения затем определяют по формулам (4.13).
Поиск по сайту: |
 (4.9)
(4.9)
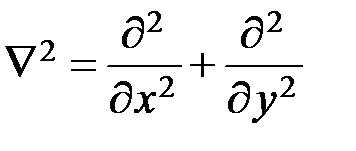 есть гармонический оператор Лапласа,
есть гармонический оператор Лапласа,  (4.10)
(4.10) (4.11)
(4.11)
 Выразим через эти перемещения деформации
Выразим через эти перемещения деформации  по формулам (4.3) и подставим их в соотношения закона Гука (4.6), а полученные выражения для напряжений
по формулам (4.3) и подставим их в соотношения закона Гука (4.6), а полученные выражения для напряжений  подставим в уравнения равновесия (4.1).
подставим в уравнения равновесия (4.1). (4.12)
(4.12)
 заметно упрощается, если ввести специальную функцию
заметно упрощается, если ввести специальную функцию  через которую выражаются все три напряжения:
через которую выражаются все три напряжения: (4.13)
(4.13) (4.14)
(4.14) (читается «набла четыре») называется бигармоническим оператором или двойным оператором Лапласа.
(читается «набла четыре») называется бигармоническим оператором или двойным оператором Лапласа. (4.15)
(4.15)