 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Матрица жёсткости дискретной схемы
Запишем узловые перемещения дискретной схемы в виде вектора в котором матрица Эта матрица составляется из матриц жёсткости отдельных КЭ. Рассмотрим пластинку, дискретная схема (ДС) которой показана на рис. 7.6, а.
Рис. 7.6. Составление матрицы жёсткости дискретной схемы: а – дискретная схема пластинки; б – местные оси конечных элементов; в – матрицы жёсткости конечных элементов; г– структура матрицы жёсткости дискретной схемы
ДС состоит из восьми треугольных КЭ (их номера указаны в скобках) и девяти узлов. Для каждого КЭ вначале составляется матрица жёсткости Ячейки матриц жёсткости КЭ переносятся в матрицу Kв соответствии с номерамистрок и столбцов. В качестве примера показаноположение ячеекa, b, c, d из матриц K3 и K5 в матрице K. Аналогичным образом поступают с остальными ячейками. На рис. 7.6, г затемнены те ячейки матрицы K,в которые попадают данные из матриц жёсткости КЭ. Если в одну и ту же позицию попадают числа из разных матриц, то они суммируются. Структура матрицы K (рис. 7.6, г) имеет вид ленты вдоль главной диагонали, а её ширина зависит от порядка нумерации узлов. Для уменьшения ширины ленты (это ускоряет решение задачи)следует минимизировать наибольшую разность между номерами узлов, «соединяемых» конечным элементом. Для решения уравнения (7.15) необходимо учесть закрепления пластинки. Наличие неподвижных опор в узлах 1 и 6 позволяет вычеркнуть из матрицы Kблочныестроки и столбцы с номерами 1 и 6. В программных комплексах формирование матрицы K производится автоматически с использованием логических процедур. Специальные алгоритмы выполняют такую нумерацию неизвестных, при которой ширина ленты матрицы Kстановитсянаименьшей.
Поиск по сайту: |
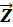 , а внешние узловые нагрузки в виде вектора
, а внешние узловые нагрузки в виде вектора 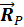 . На каждый узел передаются силы со стороны примыкающих к нему деформированных конечных элементов и действуют внешние нагрузки. Условия равновесия всех узлов можно представитьравенством
. На каждый узел передаются силы со стороны примыкающих к нему деформированных конечных элементов и действуют внешние нагрузки. Условия равновесия всех узлов можно представитьравенством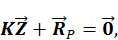 (7.15)
(7.15)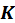 коэффициентов при неизвестных Z называется матрицей жёсткости дискретной схемы.
коэффициентов при неизвестных Z называется матрицей жёсткости дискретной схемы.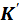 в местной системе координат (рис. 7.6, б), а затем по формуле (7.14) она переводится в общую систему координат. Если местные оси xyпараллельны общим осям XY, как для КЭ №3, то такой перевод не нужен. Матрицужёсткости
в местной системе координат (рис. 7.6, б), а затем по формуле (7.14) она переводится в общую систему координат. Если местные оси xyпараллельны общим осям XY, как для КЭ №3, то такой перевод не нужен. Матрицужёсткости