 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
МЕТОД БУБНОВА–ГАЛЁРКИНА
Метод Бубнова–Галёркинапозволяет получать приближённое аналитическое решение дифференциального уравнения. Пусть некоторая двумерная задача в области А описывается при заданных граничных условияхдифференциальным уравнением
в котором Функцию
где Две функцииF1(х,у) иF2(х,у), определённые в области А, называются ортогональными, если выполняется условие
При выполнении условия (8.1) операторL(w) будет ортогонален любой функцииF(х,у):
После подстановки приближённого выражения (8.2) в уравнение (8.1) левая часть последнего будет равна не нулю, а некоторому значению, которое называется невязкой или функцией-ошибкой, поэтому
Чтобы минимизировать невязку, сделаем её ортогональной к каждой из базисных функций:
После преобразований получается система алгебраических уравнений, из решения которой находят все коэффициентыaj. Рассмотрим примеры использования метода Бубнова–Галёркина.
L(y) = EIyIV – q = 0. Уравнение прогибов представим полиномом: y(x) = a1x2 + a2x3 + a3x4. Кинематические граничные условия (y(0) = 0, y'(0) = 0, y(l) ¹ 0, y'(l) ¹ 0) выполняются. Составим условие ортогональности дифференциального оператораL(y) и полиномау(x):
из которого следует, что Поэтому 1) х = l: Q = –EIy'" = 0; 6a2 + 24a3l = 0, откудаа2 = –4а3l. 2) х = l: М = –EIy" = 0; 2a1+ 6a2l+ 12a3l2 = 0, откудаа1 = 6а3l2. Окончательное уравнение упругой линии балки: y(x) = 6а3l2x2 – 4а3lx3 + а3x4 = Полученное решение совпадает с точным.
Пример 2. Прямоугольная тонкая пластинка, шарнирно закреплённая по контуру, находится под действием распределённой нагрузкиq(х,у) (рис. 8.2). Дифференциальный оператор уравнения равновесия бесконечно малого элемента пластинки имеет вид:
D =   цилиндрическая жёсткость пластинки. цилиндрическая жёсткость пластинки.
Зададим уравнение прогибов в виде суммы:
гдеaj – подлежащие определению множители. Базисные функцииjj назначим следующего вида:
Такие функции удовлетворяют граничным условиям – отсутствию прогибов на кромках пластинки. Целые числа m и n равны числу полуволн деформированной поверхности пластинки в направлении осей x и y соответственно (рис. 8.3).
Рис. 8.3. Поверхности, соответствующие базисным функциям (8.7)
Дифференциальный оператор (8.5) представим какL(w) = Lw +Lq, Подставим выражение (8.6) воператор (8.5) и составим условия ортогональностиL(w) к каждой базисной функцииjj:
После замены интеграла от суммы суммой интегралов приходим к системе линейных алгебраических уравнений:
где
Учитывая, что
получим
Принятые базисные функции оказываются взаимно ортогональными. Интеграл
принимаеттолько два значения: равен нулю, еслиmj ¹ mi и nj ¹ niи равен величинеab/4 Поэтому все побочные коэффициенты в системе уравнений (8.8) обращаются в ноль
в котором Рассмотрим квадратную в плане (b = a) стальную (m = 0,3) пластинку толщинойh, нагруженную равномерно распределённой по всей поверхности нагрузкой интенсивностьюq. Ограничимся одним слагаемым в формуле (8.6) приm = n = 1 (см. рис. 8.3левую схему).
Подставив выраженияD1 иDв формулу (8.11), после преобразований получим
Изогнутая поверхность пластинки описывается уравнением
в которомa1 – прогиб в центре пластинки. Вычисленное значениеa1 на 2 % отличается от приводимого в справочниках.
Выражению
можно придать вариационную трактовку. Если функцию Поэтому метод Бубнова–Галёркина можно рассматривать как выражение принципа возможных перемещений.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ 1. Какие функции называются ортогональными? 2. В чем заключается метод Бубнова–Галёркина для решения дифференциального уравнения?
Поиск по сайту: |
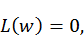 (8.1)
(8.1) – функциякоординат
– функциякоординат  и
и 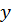 , подлежащая определению. Буквой
, подлежащая определению. Буквой 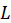 обозначен дифференциальный оператор уравнения. Уравнение (8.1) может содержать не только функцию
обозначен дифференциальный оператор уравнения. Уравнение (8.1) может содержать не только функцию  , ни и её производные разных порядков.
, ни и её производные разных порядков.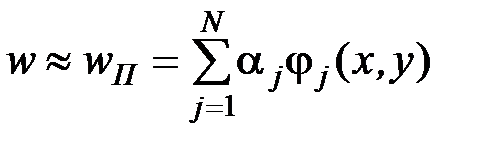 , (8.2)
, (8.2) – базисные (координатные) функции, удовлетворяющие граничным условиям; aj – неизвестные множители, которые необходимо определить.
– базисные (координатные) функции, удовлетворяющие граничным условиям; aj – неизвестные множители, которые необходимо определить. , (8.3)
, (8.3) .
. .
.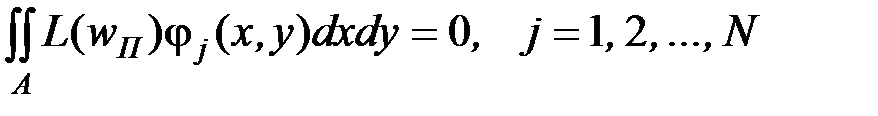 , (8.4)
, (8.4) .
. .
.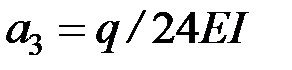 . Коэффициентыа1 иа2 находим из статических граничных условий:
. Коэффициентыа1 иа2 находим из статических граничных условий: (6l2x2 – 4lx3 + x4).
(6l2x2 – 4lx3 + x4). , (8.5)
, (8.5) , (8.6)
, (8.6) . (8.7)
. (8.7) .
. (8.8)
(8.8) (8.9)
(8.9) (8.10)
(8.10) ,
,
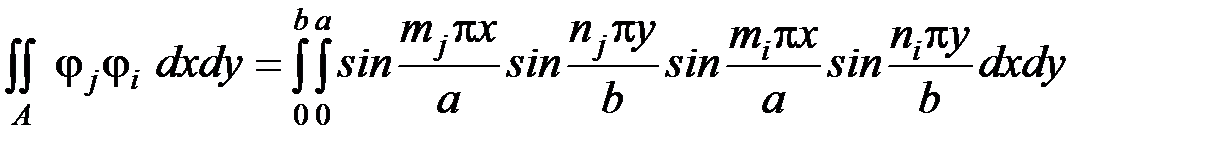
 еслиmj = mi и nj = ni.
еслиmj = mi и nj = ni. и система уравнений распадается на независимые уравнения, решением которых является выражение
и система уравнений распадается на независимые уравнения, решением которых является выражение (8.11)
(8.11) . (8.12)
. (8.12)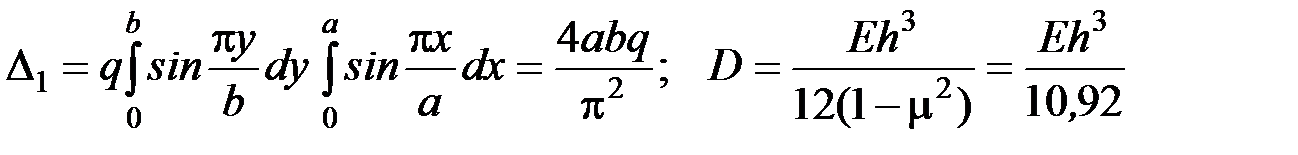 .
. .
. .
.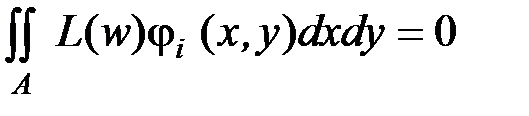 .
. рассматривать как некоторое обобщённое перемещение, а оператор
рассматривать как некоторое обобщённое перемещение, а оператор  как описание нагрузки, которая соответствует обобщённому перемещению, то указанное выражение есть работа обобщённой нагрузки на обобщённом перемещении, равная нулю для системы, находящейся в равновесии.
как описание нагрузки, которая соответствует обобщённому перемещению, то указанное выражение есть работа обобщённой нагрузки на обобщённом перемещении, равная нулю для системы, находящейся в равновесии.