|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Моменты инерции относительно параллельных осей. Момент инерции относительно оси, проходящей через начало координат⇐ ПредыдущаяСтр 20 из 20
Приведем без доказательства формулы, позволяющие вычислять элементы тензора инерции при переходе от одних координатных осей к другим. 6.3.1. Связь между осевыми моментами инерции,вычисленными относительно параллельных осей, одна из которых является центральной, дается теоремой Гюйгенса – Штейнера: момент инерции
где 6.3.2. Момент инерции относительно оси, проходящей через начало координат,и составляющей с осями
При этом углы
6.3.3. Вычисление моментов инерции относительно произвольной осиосуществляется комбинированием формул (6.4) и (6.5). ПРИМЕР 6.1. Для ротора в виде тонкого однородного диска массы а) ось вращения Из таблицы 6.1 для ротора в виде диска осевой момент инерции относительно центральной оси
По (6.4) для этого случая имеем б) ось вращения
Тогда по (6.5) для этого случая имеем
в) ось вращения Очевидно, что последний случай можно представить как совокупность двух предыдущих, т.е. где
Вопросы и задачи для самоконтроля 1. Запишите формулы для вычисления полярного, осевых и центробежных моментов инерции твердого тела. 2. Какой из моментов инерции является мерой инерции твердого тела при его вращении вокруг оси? 3. Что такое радиус инерции твердого тела и что он характеризует? Как выглядит тензор инерции в общем случае (если оси координат – главные оси инерции)? 4. Сформулируйте теорему Гюйгенса – Штейнера о вычислении осевого момента относительно параллельной оси. 5. Как вычислить момент инерции твердого тела относительно оси, если она проходит через начало координат (углы между нею и осями координат, а так же все элементы тензора инерции твердого тела заданы)? 6. Как вычислить моменты инерции твердого тела, если его можно мысленно разделить на типовые элементы? 7. Какие экспериментальные методы определения осевых моментов инерции вам известны? Каков алгоритм действий в каждом из них? 8. Решите следующие задачи из [2] : 34.7; 34.10; 34.11; 34.18; 34.31.
СПИСОК ЛИТЕРАТУРЫ
1. Н.В. Бутенин, Я.Л. Лунц, Д.Р.Меркин., Курс теоретической механики, Т.2, Наука, Москва, 1971г. 2. Мещерский И.В. Задачи по теоретической механике. Лань, Москва, 2002 г. 3. Тарг С.М.Краткий курс теоретической механики. Высшая школа, Москва, 1986 г. 4. Яблонский А.А. Курс теоретической механики, Часть 2, Высшая школа, Москва, 1977 г. 5. Чувиковский В.С. Численные методы расчетов в строительной механике корабля., Л., Судостроение, 1976 г. 6. Мелконян А.Л., Рощанский В.И., Черныш А.А. Теоретическая механика. Часть 1. Кинематика. Учебное пособие, Издательство ЛКИ, Ленинград, 1989 г. 7. Мелконян А.Л., Рощанский В.И., Черныш А.А. Теоретическая механика. Часть 3. Динамика. Учебное пособие, Издательство СПбГМТУ, Санкт-Петербург, 1996 г. 8. Мелконян А.Л. Численное моделирование процесса движения материальной точки. Методические указания. Издательство СПбГМТУ, Санкт-Петербург, 2005 г. 9. Мелконян А.Л., Черныш А.А. Динамическое уравновешивание тела, вращающегося вокруг неподвижной оси. Методические указания к лабораторным работам., Издательство СПбГМТУ, Санкт-Петербург, 1997г. 10.Матлах А.П., Мелконян А.Л., Плотников А.М., Черныш А.А. Моменты инерции твердого тела. Методические указания к лабораторным работам, Издательство ЛКИ, Ленинград, 1989 г.
Поиск по сайту: |
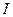 тела, вычисленный относительно некоторой оси, равен сумме момента инерции
тела, вычисленный относительно некоторой оси, равен сумме момента инерции  тела относительно оси, проходящей через центр масс параллельно данной, и произведения массы
тела относительно оси, проходящей через центр масс параллельно данной, и произведения массы 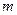 тела на квадрат расстояния между осями:
тела на квадрат расстояния между осями: , (6.4)
, (6.4)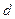 - кратчайшее расстояние между осями.
- кратчайшее расстояние между осями.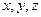 углы
углы 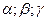 соответственно, вычисляется как
соответственно, вычисляется как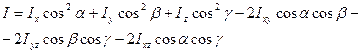 (6.5)
(6.5)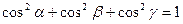 .
.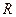 определить момент инерции относительно оси вращения
определить момент инерции относительно оси вращения 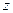 если
если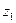 перпендикулярна плоскости диска, но центр масс С находится на расстоянии
перпендикулярна плоскости диска, но центр масс С находится на расстоянии 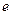 от оси вращения (рис.6.2).
от оси вращения (рис.6.2).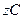 будет
будет 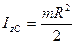 .
.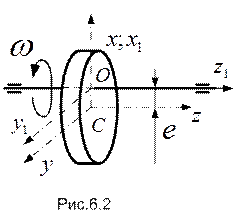
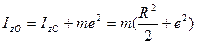 .
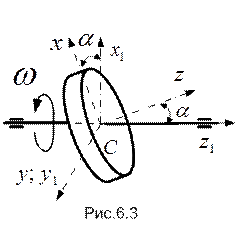
.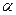 (рис.6.3). При этом угол с осью
(рис.6.3). При этом угол с осью 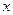 будет (
будет ( 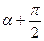 ), а с осью
), а с осью 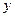 будет
будет 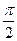 .
.
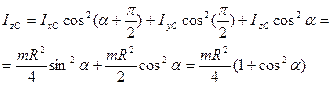
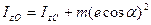 ,
,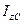 - осевой момент относительно центральной оси
- осевой момент относительно центральной оси 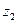 , вычисленный в предыдущем случае. Тогда
, вычисленный в предыдущем случае. Тогда