 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Теоремы об изменении количества движения и кинетического момента механической системы при ударе
Рассуждения и действия, аналогичные выполненным в предыдущих параграфах для материальной точки, позволяют получит формулы для общих теорем механики при ударе для механической системы. Так теоремы о движении центра масс и об изменении количества движения в интегральной форме можно записать в виде
где Интегральная форма теоремы об изменении кинетического момента, записанная для неподвижного центра, будет
где Если движение механической системы представить как сумму поступательного движения с кинематическими характеристиками центра масс и сферического движения относительно центра масс, то запись теоремы об изменении кинетического момента будет иметь структуру выражения (5.12), т.е.
где Для твердого тела удобно выбрать координатную систему, жестко связанную с телом; начало координат следует поместить в неподвижную точку (если она есть) либо в центр масс. Тогда, на основании (5.12) либо (5.13) и (2.16), можно записать систему скалярных уравнений
В этих уравнениях Если оси координат будут главными осями инерции, то при Если тело имеет плоскость материальной симметрии, параллельно которой происходит движение и все ударные силы лежат в этой плоскости, то из трех уравнений остается одно
где ось ПРИМЕР 5.1. Однородный стержень АО массы На горизонтальной гладкой плоскости на одной вертикали с шарниром О находится брусок массы РЕШЕНИЕ. Определим скорость Тогда Поскольку удар абсолютно неупругий (
Тогда окончательно имеем
Поиск по сайту: |
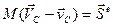 , (5.11)
, (5.11) - масса всей механической системы,
- масса всей механической системы, 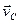 и
и  - скорость центра масс до и после удара, а
- скорость центра масс до и после удара, а  - главный импульс внешних ударных сил (импульс внешних неударных сил при ударе обращается в нуль). Поскольку перемещения точек, к которым приложены ударные силы, равны нулю, то центр масс при ударе не меняет своего положения. Скорость центра масс меняется мгновенно.
- главный импульс внешних ударных сил (импульс внешних неударных сил при ударе обращается в нуль). Поскольку перемещения точек, к которым приложены ударные силы, равны нулю, то центр масс при ударе не меняет своего положения. Скорость центра масс меняется мгновенно.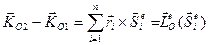 , (5.12)
, (5.12)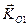 и
и 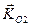 - кинетический момент точек механической системы относительно неподвижного центра О до и после удара, а
- кинетический момент точек механической системы относительно неподвижного центра О до и после удара, а  - главный момент всех внешних импульсов ударных сил относительно точки О.
- главный момент всех внешних импульсов ударных сил относительно точки О. , (5.13)
, (5.13)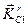 и
и  - кинетический момент точек механической системы до и после удара, вычисленные относительно движущегося центра масс С, а
- кинетический момент точек механической системы до и после удара, вычисленные относительно движущегося центра масс С, а 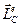 - вычисленный относительно точки С главный момент всех внешних импульсов ударных сил.
- вычисленный относительно точки С главный момент всех внешних импульсов ударных сил.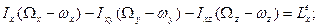

 . (5.14)
. (5.14) и
и  - проекции вектора угловой скорости тела в начале и в конце удара на
- проекции вектора угловой скорости тела в начале и в конце удара на 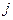 - ю координатную ось,
- ю координатную ось,  - соответствующий момент инерции, а
- соответствующий момент инерции, а  - проекция момента внешних ударных сил на
- проекция момента внешних ударных сил на  и выражения (5.14) существенно упростятся.
и выражения (5.14) существенно упростятся.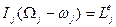 , (5.15)
, (5.15) , в точке О прикреплен к потолку цилиндрическим шарниром, а в точке А - нитью. В начальный момент времени стержень занимает горизонтальное положение (рис.5.4).
, в точке О прикреплен к потолку цилиндрическим шарниром, а в точке А - нитью. В начальный момент времени стержень занимает горизонтальное положение (рис.5.4). 
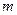 ; расстояние от шарнира до плоскости
; расстояние от шарнира до плоскости  конца А стержня до удара, для чего воспользуемся теоремой об изменении кинетической энергии в интегральной форме
конца А стержня до удара, для чего воспользуемся теоремой об изменении кинетической энергии в интегральной форме  , где конечная кинетическая энергия стержня
, где конечная кинетическая энергия стержня  , начальная -
, начальная -  , а работа активных сил
, а работа активных сил  .
. .
. ), то скорости соударяющихся тел после удара будут одинаковы, т.е.
), то скорости соударяющихся тел после удара будут одинаковы, т.е.  . Применим к механической системе из стержня и бруска теорему об изменении кинетического момента (5.12), спроецировав ее выражение на ось цилиндрического шарнира
. Применим к механической системе из стержня и бруска теорему об изменении кинетического момента (5.12), спроецировав ее выражение на ось цилиндрического шарнира 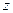 . Поскольку внешние импульсы ударных сил на эту механическую систему не действуют,
. Поскольку внешние импульсы ударных сил на эту механическую систему не действуют,  . В таком случае кинетический момент системы до удара
. В таком случае кинетический момент системы до удара  (когда брусок покоился), должен быть равен кинетическому моменту
(когда брусок покоился), должен быть равен кинетическому моменту  после удара, когда конец стержня и брусок обладают равными скоростями, т.е.
после удара, когда конец стержня и брусок обладают равными скоростями, т.е.  , где
, где  ;
; .
. .
.