 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Дифференциальные уравнения плоскопараллельного движения твердого тела
В [6] было показано, что плоскопараллельное движение твердого тела эквивалентно движению плоской фигуры в ее плоскости. Последнее по методу полюса может быть разложено на переносное (поступательное движение вместе с кинематическими характеристиками точки, принятой за полюс), и относительное (вращение вокруг полюса). Первое из них определяется изменением во времени двух координат полюса, а второе – изменением во времени угла поворота. В задачах динамики в качестве полюса удобно выбирать центр масс тела С. Для осуществления плоского движения свободного твердого тела необходимо выполнение следующих условий (см. формулы (2.10.а) и (2.26)): масса тела должна быть распределена симметрично относительно плоскости движения, проходящей через центр масс; начальные скорости точек тела должны быть расположены в плоскостях, параллельных плоскости движения; главный вектор внешних сил должен лежать в этой плоскости, а главный момент - быть перпендикулярным к ней. Для несвободного тела движение может быть плоским и в силу наложенных на него связей. Задачи динамики плоского движения тела аналогичны задачам динамики материальной точки: либо по заданным силам требуется найти законы изменения во времени координат полюса и угла поворота, либо найти силы, вызывающие заданное плоское движение твердого тела. Пусть система координат
Для описания поступательного движения тела применим теорему о движении центра масс; в проекциях на неподвижные оси получим
Дифференциальное уравнение вращения получим, применив теорему об изменении кинетического момента относительно оси
Уравнения (2.27) и (2.28) называются дифференциальными уравнениями плоскопараллельного движения твердого тела. Если тело совершает несвободное движение, то в число действующих сил необходимо включить реакции связей Уравнения плоского движения примут вид
Для получения решения задачи систему дифференциальных уравнений (2.29) следует дополнить уравнениями связей, наложенных на механическую систему. ПРИМЕР 2.6. Однородный тяжелый цилиндр радиусом РЕШЕНИЕ. Цилиндр движется под действием сил тяжести
Введем систему координат
Добавим к ним уравнения связей, наложенных на цилиндр. Во-первых, при его качении без отрыва от наклонной плоскости Первое уравнение связи следует продифференцировать по времени дважды, второе – один раз. Решив полученную систему дифференциальных уравнений относительно ускорения центра масс, получим
Интегрируя это выражение с учетом нулевых начальных условий, получим
Замечание: можно выяснить, при каких значениях угла
Поскольку условие отсутствия скольжения есть ПРИМЕР 2.7. Для механической системы, изображенной на рис.2.12, и состоящей из груза 1, прикрепленного к земле пружиной, двух соосных (насаженных неподвижно на единую ось) блоков и однородного диска, составить замкнутую систему дифференциальных уравнений движения. Жесткости пружин
РЕШЕНИЕ. Мысленно расчленим механическую систему на три тела (груз, соосные блоки и диск), приложив к каждому из тел соответствующие внешние силы (см.рис.2.12). Для описания движения тел зададим соответствующие оси координат и запишем дифференциальные уравнения движения. Уравнение для первого груза: уравнения для соосных блоков: уравнения для диска:
Полагая, что в начале координат пружины были не напряжены, для сил упругости можно записать выражения Уравнения кинематических связей будут:
В итоге получена замкнутая система из одиннадцати уравнений с одиннадцатью неизвестными. Заметим, что рассмотренная механическая система обладает двумя степенями свободы, т.е. из четырех введенных координат независимыми являются только две. Рассмотренный подход оказывается универсальным, так как позволяет решать задачи о движении механических систем, состоящих из любого числа тел и обладающих любым числом степеней свободы.
Поиск по сайту: |
 , имеющая начало в центре масс тела, движется поступательно относительно неподвижной координатной системы
, имеющая начало в центре масс тела, движется поступательно относительно неподвижной координатной системы  . Систему координат
. Систему координат  жестко свяжем с телом
жестко свяжем с телом  (рис. 2.10).
(рис. 2.10).

 . (2.27)
. (2.27)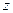 , проходящей через центра масс С перпендикулярно плоскости движения. Тогда можно записать
, проходящей через центра масс С перпендикулярно плоскости движения. Тогда можно записать . (2.28)
. (2.28) .
. ;
; ; (2.29)
; (2.29) .
. отпущен без начальной скорости и катится без скольжения по плоскости, наклоненной под углом
отпущен без начальной скорости и катится без скольжения по плоскости, наклоненной под углом 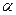 к горизонту. Найти уравнения движения цилиндра.
к горизонту. Найти уравнения движения цилиндра. , трения (сцепления)
, трения (сцепления)  и нормальной реакции
и нормальной реакции  плоскости (см. рис.2.11.).
плоскости (см. рис.2.11.).
 ;
; ;
; .
. , т.к. в процессе движения расстояние от центра масс С до наклонной плоскости не меняется и равно
, т.к. в процессе движения расстояние от центра масс С до наклонной плоскости не меняется и равно  или
или  .
. ;
;  .
.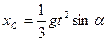 ;
; 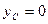 .
. .
. (здесь
(здесь  - коэффициент трения скольжения), качение без скольжения будет иметь место при
- коэффициент трения скольжения), качение без скольжения будет иметь место при  .
. и
и  , вес груза
, вес груза 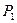 , вес блоков
, вес блоков  , их радиусы
, их радиусы 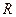 и
и  , вес диска
, вес диска  и его радиус
и его радиус  известны.
известны.
 ;
; ;
;  ;
;  ;
; ;
; ;
;  .
. ;
;  .
. или
или  ;
; или
или  .
.