 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Метод кинетостатики (принцип Даламбера)
Пусть движение произвольной точки
Перепишем его в форме
где Таким образом, для динамической задачи мы получили уравнение, которое можно трактовать как уравнение равновесия. Поступая аналогично с другими точками системы и суммируя уравнения (3.1) по индексу
Обозначив главные векторы активных сил, реакций связей и сил инерции соответственно через
Умножив векторно
Уравнения (3.2) и (3.3) представляют принцип Даламбера: в каждый момент времени главный вектор сил инерции уравновешивает главные векторы активных сил и реакций связей; точно так же главный момент сил инерции относительно некоторого центра уравновешивает главные моменты активных сил и реакций связей. Если действующие на
где Принцип Даламбера дает удобный прием решения задач динамики несвободных систем. Путем приложения к точкам механической системы фиктивных сил инерции задача динамики легко сводится к соответствующей задаче статики. Уравнения (3.2) и (3.3) либо (3.4) называют уравнениями кинетостатики. Для использования этих уравнений необходимо правильно вычислять главный вектор и главный момент сил инерции механической системы, в частности, твердого тела. Так при поступательном движении тела
при вращении тела вокруг неподвижной оси
при плоском движении тела
ПРИМЕР 3.1 (задача 41.7 из [2]). Для экспериментального определения замедления троллейбуса применяется жидкостный акселерометр, состоящий из изогнутой трубки, наполненной маслом и расположенный в вертикальной плоскости. Определить величину замедления троллейбуса при торможении, если при этом уровень жидкости в конце трубки, расположенном в направлении движения, повышается до величины
РЕШЕНИЕ. Выделим в каждом колене элементарную массу
Вынесем постоянные величины за знаки суммирования. Введем массу единицы объема
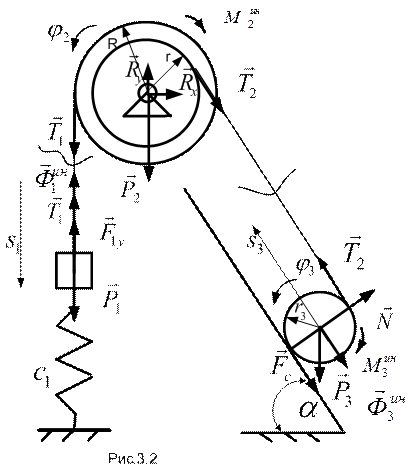
ПРИМЕР 3.2. Для механической системы из примера 2.8 найти силы натяжения нитей РЕШЕНИЕ. Воспользуемся решением примера 2.8 для получения величины ускорения первого груза
Для того, чтобы механическая система находилась в равновесии, к действующим на ее тела силам (см. рис.3.2) следует добавить соответствующие силы инерции и моменты сил инерции:
Теперь запишем уравнение равновесия первого груза:
Из него находим силу натяжения первой нити Теперь запишем уравнение равновесия для соосных блоков:
Из него находим силу натяжения второй нити
Поиск по сайту: |
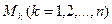 массой
массой 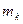 механической системы вызвано равнодействующей
механической системы вызвано равнодействующей  задаваемых сил и равнодействующей
задаваемых сил и равнодействующей  реакций связей. Тогда для
реакций связей. Тогда для  -ой точки основное уравнение динамики имеет вид
-ой точки основное уравнение динамики имеет вид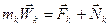 ;
;  .
. , (3.1)
, (3.1) есть сила инерции.
есть сила инерции. .
. и
и  , будем иметь
, будем иметь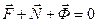 . (3.2.)
. (3.2.) на силы, входящие в (3.1), и суммируя их по
на силы, входящие в (3.1), и суммируя их по 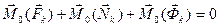 . (3.3)
. (3.3)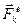 и равнодействующей внутренних сил
и равнодействующей внутренних сил  , то, с учетом свойств внутренних сил, уравнения (3.2) и (3.3) примут вид
, то, с учетом свойств внутренних сил, уравнения (3.2) и (3.3) примут вид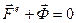 ;
; 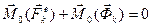 , (3.4)
, (3.4) - главный вектор внешних сил.
- главный вектор внешних сил.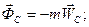




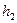 , а в противоположном конце понижается до
, а в противоположном конце понижается до  . Положение акселерометра указано на рисунке 3.1; при этом
. Положение акселерометра указано на рисунке 3.1; при этом 

 . Жидкость можно полагать находящейся в равновесии, если к действующим силам веса
. Жидкость можно полагать находящейся в равновесии, если к действующим силам веса 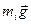 добавить силы инерции
добавить силы инерции 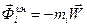 (внутренние силы взаимодействия частиц не нанесены, так как их главный вектор равен нулю). Приравняем проекции на продольные оси первого и второго участков трубки главных векторов соответствующих сил (давление столба жидкости в нижней точке первого участка трубки должно быть равно давлению столба жидкости в нижней точке второго участка). Тогда
(внутренние силы взаимодействия частиц не нанесены, так как их главный вектор равен нулю). Приравняем проекции на продольные оси первого и второго участков трубки главных векторов соответствующих сил (давление столба жидкости в нижней точке первого участка трубки должно быть равно давлению столба жидкости в нижней точке второго участка). Тогда .
. . Тогда масса жидкости в левой части трубки будет
. Тогда масса жидкости в левой части трубки будет  , главный вектор сил инерции
, главный вектор сил инерции  , а сила веса жидкости
, а сила веса жидкости  ; выражения для соответствующих величин правого участка трубки аналогичны. Подставив полученные выражения в уравнение, сократим все слагаемые на массу единицы объема. Сгруппируем слагаемые, содержащие ускорение
; выражения для соответствующих величин правого участка трубки аналогичны. Подставив полученные выражения в уравнение, сократим все слагаемые на массу единицы объема. Сгруппируем слагаемые, содержащие ускорение  в левой части равенства, не содержащие ускорения – в правой. Окончательно получим
в левой части равенства, не содержащие ускорения – в правой. Окончательно получим .
. и
и  .
. ; здесь амплитуда
; здесь амплитуда 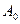 и начальная фаза
и начальная фаза 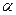 полагаются вычисленными величинами (по начальным условиям движения). Для получения ускорений других тел механической системы продифференцируем по времени уравнения кинематических связей, т.е.
полагаются вычисленными величинами (по начальным условиям движения). Для получения ускорений других тел механической системы продифференцируем по времени уравнения кинематических связей, т.е.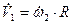 или
или  ;
; или
или 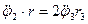 ;
;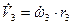 или
или 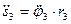 .
.

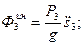

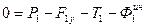 .
.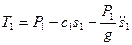 .
. .
.