 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Косой удар материальной точки о неподвижную гладкую поверхность
В случае, когда неподвижная поверхность гладкая, ее реакция и ударный импульс Тогда запись теоремы об изменении количества движения (5.2) примет вид
Проецируя (5.7) на касательную
Таким образом, касательная составляющая скорости сохраняет свою величину и направление; нормальная составляющая направление изменяет на противоположное, при этом изменение ее величины определяется величиной ударного импульса.
Если известен коэффициент восстановления Сначала воспользуемся первой формулой из (5.8): Отсюда
Для угла отражения окончательно имеем Теперь определим модуль скорости после удара:
Анализ полученных выражений показывает, что при любом не вполне упругом ударе модуль скорости отражения всегда меньше модуля скорости падения, а угол отражения больше угла падения. При абсолютно неупругом ударе точка «рикошетирует» от идеально гладкой поверхности, сохраняя лишь касательную составляющую. При абсолютно упругом ударе угол падения равен углу отражения, модуль скорости не изменяется. Для нахождения ударного импульса воспользуемся второй формулой из (5.8) . Учтем, что
Из этого соотношения видно, что максимальный ударный импульс имеет место при прямом ударе (
Потеря кинетической энергии при ударе материальной точки о неподвижную поверхность Изменение кинетической энергии при ударе определяется как разность ее значений до и после удара, т.е.
Учтем, что
Из (5.9) следует, что при абсолютно упругом ударе ( Формула (5.9) может быть записана через «потерянную скорость»
Тогда для (5.9) примет вид
Заметим, что при абсолютно неупругом ударе (
Поиск по сайту: |
направлены по нормали к ней (рис.5.3).
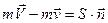. (5.7)
и нормаль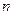 
, получим
. (5.8)
, можно найти скорость точки 
(ее модуль и угол отражения 
), а также модуль ударного импульса 
.
.
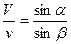. Поскольку одно из соударяющихся тел неподвижно, (5.4) принимает вид
.
.
.
. Тогда
.
).
.
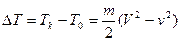. Тогда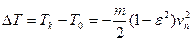
. (5.9)
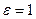) потери кинетической энергии нет, при абсолютно неупругом ударе ( 
) вся кинетическая энергия переходит в другие формы энергии (в частности, в тепловую). При не вполне упругом ударе переходит в другие формы энергии только часть кинетической энергии.
. Если учесть равенство касательных составляющих скоростей падения и отражения, для потерянной скорости можно записать выражение
.
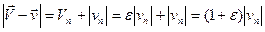. (5.10)
.