 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Гироскопический момент
Перейдем к рассмотрению обратной задачи динамики гироскопа. Пусть гироскоп с двумя степенями свободы (см. рис.4.1.б) вращается с угловой скоростью
Отсюда следует правило Грюэ – Жуковского: при сообщении оси быстро вращающегося гироскопа принудительной прецессии его ось стремиться кратчайшим путем установиться таким образом, чтобы направления векторов ПРИМЕР 4.2. Определить усилия гироскопической природы, действующие на опоры ротора турбины, при циркуляции катера (см. рис.4.2). Осевой момент инерции ротора турбины РЕШЕНИЕ. Подставляя в (4.6) значение гироскопического момента
Заметим, что найденные реакции могут существенно превышать реакции от силы веса турбины. Действуя через подшипники на корпус катера, они могут вызвать его дифферент. Подобный эффект наблюдается и у винтовых самолетов на виражах.
Вопросы и задачи для самоконтроля 1. Сформулируйте основное допущение элементарной теории гироскопов. 2. Запишите теорему об изменении кинетического момента в трактовке Резаля. 3. Как найти угловую скорость прецессии оси гироскопа, если известен момент внешних сил, на него действующих (осевой момент инерции гироскопа и скорость его вращения вокруг собственной оси заданы)? 4. Что такое гироскопический момент и как его вычислить, если известны осевой момент инерции гироскопа, а так же угловые скорости прецессии и собственного вращения. 5. Решите следующие задачи из [2] : 40.1; 40.4; 40.8; 40.12.
Элементарная теория удара Основные допущения При контакте двух тел в точке соприкосновения возникают равные противоположно направленные силы действия и противодействия. Закон изменения этих сил приведен на рис.5.1. Импульс силы
Поскольку при ударе время действия силы несоизмеримо меньше промежутков времени, для которых обычно рассматривается движение, величину
Найдем, как изменяется скорость и положение материальной точки при действии ударной силы (мгновенного импульса). Для этого запишем в интегральной форме теорему об изменении ее количества движения
где Перепишем (5.2) в виде
где Если на точку действует ударная сила
На этом основании при исследовании процессов, происходящих при ударе, медленно изменяющиеся ограниченные по модулю силы не учитываются. Все сказанное справедливо для любых сил, изменение которых происходит по закону, изображенному на рис.5.1 (например, при взрыве).
Поиск по сайту: |
 вокруг собственной оси симметрии АВ, а ось, в свою очередь, вращается с угловой скоростью
вокруг собственной оси симметрии АВ, а ось, в свою очередь, вращается с угловой скоростью  вокруг вертикальной оси. Момент внешних сил, под действием которого прецессирует гироскоп, создается силами, приложенными к оси гироскопа со стороны подшипников А и В. По третьему закону Ньютона на подшипники со стороны оси гироскопа действуют равные и противоположно направленные силы
вокруг вертикальной оси. Момент внешних сил, под действием которого прецессирует гироскоп, создается силами, приложенными к оси гироскопа со стороны подшипников А и В. По третьему закону Ньютона на подшипники со стороны оси гироскопа действуют равные и противоположно направленные силы  и
и  . Главный момент этих сил относительно неподвижной точки О называется гироскопическим моментом. Он может быть вычислен на основании (4.3) и (4.4):
. Главный момент этих сил относительно неподвижной точки О называется гироскопическим моментом. Он может быть вычислен на основании (4.3) и (4.4): . (4.6)
. (4.6) , угловая скорость его вращения
, угловая скорость его вращения  , радиус циркуляции
, радиус циркуляции 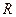 и скорость движения катера
и скорость движения катера  известны.
известны. (здесь
(здесь  - модуль сил
- модуль сил  ) и
) и  , находим:
, находим:  .
.
 за время ее действия
за время ее действия  определяется как
определяется как . (5.1)
. (5.1) конечной величины (5.1). Мгновенное действие силы, при котором ее импульс имеет конечную величину, называется ударом, а соответствующая сила – ударной силой.
конечной величины (5.1). Мгновенное действие силы, при котором ее импульс имеет конечную величину, называется ударом, а соответствующая сила – ударной силой.
 или
или 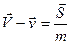 , (5.2)
, (5.2)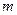 - масса точки, а
- масса точки, а  и
и  - ее скорость в конце и в начале удара, соответственно. Так как импульс
- ее скорость в конце и в начале удара, соответственно. Так как импульс  имеет конечную величину, то при ударе скорость точки мгновенно изменяется на конечную величину.
имеет конечную величину, то при ударе скорость точки мгновенно изменяется на конечную величину. . Разделив переменные и взяв интегралы от обеих частей равенства, получим (используя теорему о среднем из курса интегрального исчисления)
. Разделив переменные и взяв интегралы от обеих частей равенства, получим (используя теорему о среднем из курса интегрального исчисления) , (5.3)
, (5.3) и
и  - радиусы – векторы точки в начальный и конечный момент времени, а
- радиусы – векторы точки в начальный и конечный момент времени, а  - среднее значение импульса
- среднее значение импульса  на промежутке [0;
на промежутке [0;  перемещение точки
перемещение точки  ).
). и обычная медленно меняющаяся во времени сила
и обычная медленно меняющаяся во времени сила  , то их суммарный импульс
, то их суммарный импульс  за время
за время  , где последний интеграл записан по теореме о среднем. Очевидно, что при
, где последний интеграл записан по теореме о среднем. Очевидно, что при  .
.