 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Теорема об изменении кинетической энергии
2.6.1. Кинетическая энергия механической системы.Кинетической энергией
Кинетической энергией механической системы называют сумму кинетических энергий включенных в эту систему материальных точек:
В тех случаях, когда масса системы распределена непрерывно, суммирование в выражении (2.31) заменяют интегрированием по области распределения. Найдем связь между значениями кинетической энергии механической системы в двух системах отсчета, одна из которых неподвижна, а другая движется поступательно со скоростью
Тогда вместо (2.31) получим
Здесь Если за начало координат подвижной системы принимается центр масс механической системы С, то выражение (2.33) упрощается (теорема Кенига):
Использование выражений (2.31) и (2.34) позволяет сформулировать следующие правила вычисления кинетической энергии твердого тела: при поступательном движении тела массой
при вращении с угловой скоростью
при плоскопараллельном движении твердого тела с угловой скоростью
при сферическом движении с угловой скоростью вращения и значении момента инерции тела
в общем случае движения твердого тела
Здесь момент инерции В качестве примера вычислим кинетическую энергию механической системы, изображенной на рис.2.11, как сумму кинетических энергий тел ее формирующих. В этом случае
С учетом уравнений кинематических связей
2.6.2. Энергетические характеристики. К энергетическим характеристикам силы относят ее мощность, работу и потенциальную энергию. Мощностью
Работа силы
Работой
Работа момента пары сил вычисляется аналогично. Потенциальная энергия
При выполнении условия (2.43) говорят, что сила потенциальна. Сопоставление формул (2.41) и (2.43) позволяет записать соотношения, связывающие проекции силы на оси выбранной координатной системы с функцией
Если точка приложения силы переместилась из положения
Заметим (см. формулы (2.41), (2.44) и (2.45)), что потенциальная энергия определена с точностью до постоянного слагаемого; отмеченная особенность позволяет полагать потенциальную энергию равной нулю в выбираемой нами точке (например, в начале координат). В последнем случае формула (2.45) принимает вид
Иными словами – потенциальная энергия равна работе сил по переводу системы из отклоненного положения в начальное. В том случае, когда для совокупности сил, действующих на механическую систему, можно записать выражение потенциальной энергии
В качестве примера вычислим потенциальную энергию для трех частных, но важных для технических приложений, случаев: действуют сила тяжести, центральная сила и сила упругости пружины. Для силы тяжести
Для центральной силы
Силу упругости пружины можно считать центральной силой, направленной к началу координат; в случае прямой пропорциональности между величиной силы
При определении энергетических характеристик системы сил суммируют соответствующие характеристики для всех сил, действующих на механическую систему.
2.6.3. Теорема об изменении кинетической энергии.Умножим уравнения (2.5) скалярно на скорость
где Заметим, что если связи между телами, формирующими систему, допускают деформацию (см. пружину жесткостью Изменив порядок суммирования и дифференцирования в левой части равенства, ее можно привести к виду
Окончательно имеем запись теоремы об изменении кинетической энергии механической системы в дифференциальной форме:
- производная по времени от кинетической энергии механической системы равна мощности всех действующих сил. В дифференциальной форме, основанной на понятии работы силы за элементарный промежуток времени, получим
Интегрируя (2.52) на интервале времени [0;
где В частном случае, когда для совокупности внешних и внутренних сил системы можно записать выражение потенциальной энергии
вместо (2.52) имеем соотношение
В такой системе выполняется закон сохранения полной механической энергии
а сама система называется консервативной. ПРИМЕР 2.8. Для механической системы, изображенной на рис.2.13, и отличающейся от рассмотренной в примере 2.7 отсутствием пружины жесткостью
РЕШЕНИЕ. Для решения задачи воспользуемся теоремой об изменении кинетической энергии в дифференциальной форме (2.51). Мысленно освободимся от связей, приложив к телам механической системы соответствующие реакции (см.рис.2.13). Составим выражение для кинетической энергии механической системы:
Запишем уравнения кинематических связей:
При записи учтено, что мгновенный центр скоростей диска, катящегося без скольжения, расположен в точке его соприкосновения с плоскостью. В формулу для кинетической энергии подставим угловые скорости вращения соосных блоков, диска и скорость центра масс диска, выраженные через скорость первого груза (в отличие от механической системы из примера 2.7, рассматриваемая система имеет одну степень свободы); тогда
При получении результата учтено, что осевой момент инерции однородного диска Продифференцировав выражение для кинетической энергии по времени, получим левую часть равенства (2.51):
Отметим, что в рассматриваемой системе внутренние связи не деформируемы, поэтому мощность внутренних сил должна быть равна нулю. Запишем выражение для мощности внешних сил:
при записи учтено, что сила упругости В выражение для мощности подставим скорость центра диска, выраженную через скорость первого груза; тогда
Приравняем выражения для левой и правой частей равенства (2.51); сократим их на
где Полученное неоднородное дифференциальное уравнение описывает гармонические колебания с частотой
где
Вопросы и задачи для самоконтроля 1. Какими свойствами обладают внутренние силы механической системы? 2. Как найти положение центра масс механической системы? 3. Сформулируйте теорему о движении центра масс механической системы и ее следствия. 4. Как вычислить количество движения механической системы? Сформулируйте теорему об изменении количества движения механической системы в дифференциальной (интегральной) форме и ее следствия. 5. Как вычислить кинетический момент механической системы относительно неподвижного центра (относительно центра масс)? 6. Сформулируйте теорему об изменении кинетического момента механической системы относительно неподвижного центра (центра масс) в дифференциальной (интегральной) форме и ее следствия. 7. Запишите дифференциальные уравнения поступательного, вращательного и плоского движения твердого тела. Обратите внимание на одинаковость структур формул для поступательного и вращательного движений. 8. Как вычисляется и что характеризует осевой момент инерции масс твердого тела? 9. Как вычислить кинетическую энергию механической системы? Как вычислить работу переменной силы? Какова связь мощности и работы силы? Сформулируйте теорему об изменении кинетической энергии механической системы в дифференциальной (интегральной) форме, если действующие силы разделить на внешние и внутренние (на задаваемые и реакции связей). 10. Решите следующие задачи из [2] : 35.4; 35.21; 36.9; 36.13; 37.6; 37.14; 37.33; 37.44; 37.53; 38.24; 38.31; 39.19; 39.15.
Метод кинетостатики.
Поиск по сайту: |
 материальной точки массы
материальной точки массы  , движущейся со скоростью
, движущейся со скоростью  , называют величину
, называют величину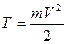 . (2.30)
. (2.30) . (2.31)
. (2.31) . В этом случае скорость
. В этом случае скорость  точки в неподвижной координатной системе и относительная скорость
точки в неподвижной координатной системе и относительная скорость  связаны соотношением
связаны соотношением . (2.32)
. (2.32) . (2.33)
. (2.33) - относительная скорость центра масс;
- относительная скорость центра масс;  - кинетическая энергия механической системы в подвижной системе координат.
- кинетическая энергия механической системы в подвижной системе координат. . (2.34)
. (2.34) со скоростью
со скоростью 
 ; (2.35)
; (2.35) вокруг неподвижной оси
вокруг неподвижной оси 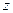 тела с моментом инерции
тела с моментом инерции 
 ; (2.36)
; (2.36)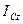 относительно оси, перпендикулярной плоскости движения, и значении
относительно оси, перпендикулярной плоскости движения, и значении  момента инерции относительно мгновенной оси вращения
момента инерции относительно мгновенной оси вращения ; (2.37)
; (2.37) относительно мгновенной оси вращения
относительно мгновенной оси вращения 
 ; (2.38)
; (2.38) . (2.39)
. (2.39) вычисляется относительно мгновенной оси
вычисляется относительно мгновенной оси  такого сферического движения тела, которое оно совершает в системе осей, перемещающихся поступательно вместе с центром масс С.
такого сферического движения тела, которое оно совершает в системе осей, перемещающихся поступательно вместе с центром масс С. .
. и
и  выражение для кинетической энергии рассматриваемой механической системы с двумя степенями свободы может быть записано через любые две переменные, принятые за независимые. Например, если полагать независимыми
выражение для кинетической энергии рассматриваемой механической системы с двумя степенями свободы может быть записано через любые две переменные, принятые за независимые. Например, если полагать независимыми  и
и  , то выражение для кинетической энергии примет вид
, то выражение для кинетической энергии примет вид .
. силы
силы  , точка приложения которой движется со скоростью
, точка приложения которой движется со скоростью  . (2.40)
. (2.40) на элементарном интервале времени
на элементарном интервале времени  и соответствующем этому промежутку времени элементарному смещению
и соответствующем этому промежутку времени элементарному смещению  точки приложения определяется по правилу
точки приложения определяется по правилу . (2.41)
. (2.41) силы на конечном интервале времени [0;
силы на конечном интервале времени [0;  ] и соответствующем изменении радиуса – вектора точки приложения этой силы от
] и соответствующем изменении радиуса – вектора точки приложения этой силы от  до
до 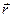 называют величину
называют величину . (2.42)
. (2.42) определена только в тех случаях, когда выражение (2.41) представляет собой полный дифференциал
определена только в тех случаях, когда выражение (2.41) представляет собой полный дифференциал  . (2.43)
. (2.43) ;
;  ;
;  . (2.44)
. (2.44) в положение
в положение  , то путем интегрирования (2.43) можно получить
, то путем интегрирования (2.43) можно получить . (2.45)
. (2.45) . (2.46)
. (2.46) ;
;  ;
; 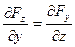 . (2.47)
. (2.47) выполняются критерии (2.47); тогда, в соответствии с формулами (2.42) и (2.46), имеем
выполняются критерии (2.47); тогда, в соответствии с формулами (2.42) и (2.46), имеем . (2.48)
. (2.48) , модуль которой зависит от расстояния
, модуль которой зависит от расстояния  до начала координат, так же выполняются критерии (2.47), поэтому
до начала координат, так же выполняются критерии (2.47), поэтому . (2.49)
. (2.49) и удлинением
и удлинением 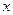 пружины имеем
пружины имеем  . В этом случае
. В этом случае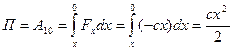 . (2.50)
. (2.50) ,
, и
и  - мощности внешних и внутренних сил, действующих на механическую систему.
- мощности внешних и внутренних сил, действующих на механическую систему. в примере 2.7), то точки приложения равных и противоположно направленных внутренних сил
в примере 2.7), то точки приложения равных и противоположно направленных внутренних сил  имеют различные скорости, вследствие чего их суммарная мощность не будет равной нулю.
имеют различные скорости, вследствие чего их суммарная мощность не будет равной нулю. .
.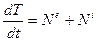 . (2.51)
. (2.51) . (2.52)
. (2.52) , (2.53)
, (2.53) ;
;  ;
;  ;
;  .
. ,
,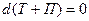 . (2.54)
. (2.54) ,
,
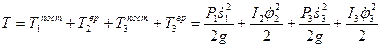 .
. или
или  ;
; или
или  ;
; или
или  .
. .
. .
.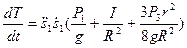 .
.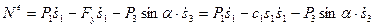 ,
, , а мощность силы сцепления, приложенной в мгновенном центре скоростей, равна нулю.
, а мощность силы сцепления, приложенной в мгновенном центре скоростей, равна нулю. .
. . Перенесем переменные величины в левую часть равенства и поделим все слагаемые на постоянный коэффициент при ускорении первого груза. Окончательный вид искомого дифференциального уравнения будет
. Перенесем переменные величины в левую часть равенства и поделим все слагаемые на постоянный коэффициент при ускорении первого груза. Окончательный вид искомого дифференциального уравнения будет ,
, .
. около смещенного на величину
около смещенного на величину  положения (положения статического равновесия механической системы), т.е.
положения (положения статического равновесия механической системы), т.е. ,
, , а постоянные амплитуда
, а постоянные амплитуда 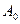 и начальная фаза
и начальная фаза 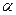 определяются из начальных условий движения.
определяются из начальных условий движения.