 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Статическая и динамическая балансировка ротора
Ротором будем называть твердое тело, имеющего неподвижную ось вращения. Очевидно, что равенство нулю проекций на оси
Решая систему (3.8) относительно координат центра масс, получим:
т.е. центр масс ротора должен располагаться на оси вращения. Решая систему (3.9) относительно центробежных моментов инерции, получим:
т.е. ось вращения ротора Объединение решений приводит к выводу: дополнительные динамические реакции отсутствуют, если ось вращения является главной центральной осью инерции ротора. Условия (3.10) позволяют произвести балансировку любого ротора. Эта задача сводится к определению величин уравновешивающих масс и координат точек их расположения. Поскольку искомые величины не должны зависеть от кинематических характеристик вращательного движения тела, для ротора будем рассматривать только его равномерное вращение ( Статическая неуравновешенность свойственна ротору, главная центральная ось Заметим, что статическая неуравновешенность ротора может быть обнаружена и без приведения ротора во вращение; при этом ротор сам стремиться повернуться под действием момента силы веса. Именно это обстоятельство и определило название рассмотренной неуравновешенности. Моментная неуравновешенность ротора имеет место в случае, когда его центр масс С находится в точке пересечения главной центральной оси с осью вращения ( Динамическая неуравновешенность является совокупностью двух предыдущих. Очевидно, что она устраняется не менее чем двумя корректирующими массами. Следовательно, при ликвидации любого типа неуравновешенности главная центральная ось ротора совмещается с осью вращения. В этом случае ротор называется полностью сбалансированным. В [9] вопросы балансировки роторов освещены более подробно.
Вопросы и задачи для самоконтроля 1. Сформулируйте метод кинетостатики. 2. Как найти динамические реакции, возникающие на оси вращающегося ротора? 3. Что называют статической балансировкой ротора и как она выполняется? 4. Что называют динамической балансировкой ротора и как она выполняется? 5. Сформулируйте условия, при которых динамические реакции в подшипниках вращающегося ротора будут отсутствовать. 6. Решите следующие задачи из [2] : 41.17; 41.19; 41.23;42.4; 42.13.
Поиск по сайту: |
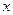 и
и 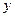 связанной с ротором координатной системы дополнительных опорных реакций подшипников будет иметь место при равенстве нулю соответствующих проекций главного вектора и главного момента сил инерции. Тогда при любых значениях угловой скорости
связанной с ротором координатной системы дополнительных опорных реакций подшипников будет иметь место при равенстве нулю соответствующих проекций главного вектора и главного момента сил инерции. Тогда при любых значениях угловой скорости  и углового ускорения
и углового ускорения  должны удовлетворяться две системы однородных уравнений:
должны удовлетворяться две системы однородных уравнений:
 (3.8)
(3.8)
 . (3.9)
. (3.9) (3.10.а)
(3.10.а) ; (3.10.б)
; (3.10.б)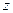 должна быть его главной осью инерции.
должна быть его главной осью инерции.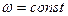 ).
).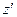 которого параллельна оси вращения
которого параллельна оси вращения 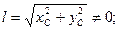
 ). В таком случае дополнительные динамические опорные реакции образуют пару сил, которая вращается вместе с ротором. Поскольку пару сил можно уравновесить только другой парой, устранение моментной неуравновешенности осуществляется не менее чем двумя корректирующими массами.
). В таком случае дополнительные динамические опорные реакции образуют пару сил, которая вращается вместе с ротором. Поскольку пару сил можно уравновесить только другой парой, устранение моментной неуравновешенности осуществляется не менее чем двумя корректирующими массами.