 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Коэффициент восстановления при ударе
Процесс удара можно разбить на две фазы. В первой фазе тела сближаются по линии общей нормали, при этом проекция на нормаль относительной скорости точки контакта уменьшается до нуля, а тела деформируются. Во второй фазе тела восстанавливают свою форму, а проекция на нормаль относительной скорости начинает возрастать, изменив знак. Как правило, ее значение, достигнутое по окончании второй фазы, не превышает начального значения на первой фазе. Как показывают опыты, в первом приближении можно принять гипотезу Ньютона: отношение модуля нормальной составляющей относительной скорости точки контакта после удара к ее величине до удара есть некоторая постоянная величина, называемая коэффициентом восстановления Если Заметим, что абсолютно неупругий удар не имеет второй фазы и после удара тела либо движутся вместе, либо одно тело скользит по поверхности другого. Обозначим через Пусть скорости
Заметим, что в таком случае удар называется прямым (в противном случае удар оказывается косым). Если центры масс тел По определению коэффициента восстановления можно записать
или, учитывая изменение направления относительной скорости,
Если для каждого из тел ввести свой единичный вектор внутренней нормали (
Коэффициент восстановления может быть получен в результате достаточно простого эксперимента – падения шарика на неподвижную (
Значения коэффициента восстановления для различных пар соударяющихся тел приводятся в справочниках. Например, при соударении стекла со стеклом
Поиск по сайту: |
 . Эта величина характеризует физические свойства соударяющихся тел; она не зависит от их масс и относительных скоростей.
. Эта величина характеризует физические свойства соударяющихся тел; она не зависит от их масс и относительных скоростей.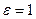 , удар называется абсолютно упругим, если
, удар называется абсолютно упругим, если  , то удар абсолютно неупругий, если
, то удар абсолютно неупругий, если  - не вполне упругий, или просто упругий.
- не вполне упругий, или просто упругий.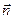 единичный вектор общей нормали двух соударяющихся тел (она называется линией удара). Пренебрегая трением, будем считать, что ударные силы и их импульсы направлены по общей нормали
единичный вектор общей нормали двух соударяющихся тел (она называется линией удара). Пренебрегая трением, будем считать, что ударные силы и их импульсы направлены по общей нормали 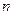 к поверхностям соударяющихся тел.
к поверхностям соударяющихся тел. и
и  точек контакта первого и второго тел в начале удара направлены по линии удара; по этой же линии будут направлены скорости
точек контакта первого и второго тел в начале удара направлены по линии удара; по этой же линии будут направлены скорости  и
и  соответствующих точек в конце удара (рис.5.2).
соответствующих точек в конце удара (рис.5.2).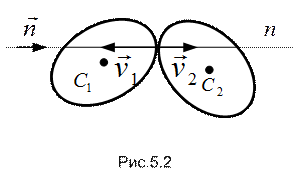
 и
и 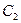 будут расположены на линии удара - удар называется центральным. Если векторы скоростей совпадают с линией удара, проходящей через центры масс тел, удар называется прямым центральным.
будут расположены на линии удара - удар называется центральным. Если векторы скоростей совпадают с линией удара, проходящей через центры масс тел, удар называется прямым центральным. (5.4)
(5.4) . (5.5)
. (5.5) ), формулу (5.5) можно переписать в виде
), формулу (5.5) можно переписать в виде . (5.6)
. (5.6)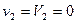 ) плиту. Зная высоту
) плиту. Зная высоту  , с которой без начальной скорости был отпущен шарик, и измерив высоту
, с которой без начальной скорости был отпущен шарик, и измерив высоту  , на которую он поднимется после отскока, получим
, на которую он поднимется после отскока, получим .
. ; стали со сталью
; стали со сталью 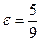 ; дерева с деревом
; дерева с деревом  .
.