 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Косой центральный удар двух шаров
Для двух шаров, изображенных на рис.5.6, известны массы
Воспользуемся теоремой об изменении количества движения (5.11). В отсутствии импульсов внешних сил имеем
Теперь для каждого из шаров составим выражение для коэффициента восстановления при ударе как отношение проекций на ось
Полученные выражения позволяют вычислить проекции на ось
Условие сохранения проекций на ось
Учтем, что
Теперь для вычисления соответствующих углов получим выражения
Для нахождения численных значений скоростей центров шаров после удара можно воспользоваться записанными формулами
Вопросы и задачи для самоконтроля 1. Какое взаимодействие принято называть ударом? Как изменяются положение и скорость точек соударяющихся тел? Как учитывается действие сил, незначительно изменяющихся в процессе удара? 2. Что такое коэффициент восстановления при ударе? Какой удар называют абсолютно упругим (неупругим)? Какие величины следует измерить для вычисления коэффициента восстановления при падении шарика на горизонтальную неподвижную поверхность? 3. Какой удар называется косым? Как найти скорость и угол отскока шарика от гладкой неподвижной поверхности, если скорость до удара, угол падения и коэффициент восстановления известны? 4. Как вычислить величину кинетической энергии, перешедшей в другие виды энергии вследствие удара? 5. Сформулируйте теоремы об изменении количества движения и кинетического момента механической системы для процесса удара. 6. Решите следующие задачи из [2] : 44.2; 44.6; 44.9; 44.17; 44.25.
Теория моментов инерции твердого тела
Поиск по сайту: |
 и
и  , скорости их движения
, скорости их движения  и
и  , а так же их направления (углы
, а так же их направления (углы 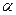 и
и  с линией общей нормали) до удара, найти величины и направления соответствующих скоростей после удара.
с линией общей нормали) до удара, найти величины и направления соответствующих скоростей после удара. Из определения центрального удара
Из определения центрального удара  , так как центры масс шаров (и, следовательно, центр масс механической системы) лежат на линии общей нормали. Тогда по (5.13)
, так как центры масс шаров (и, следовательно, центр масс механической системы) лежат на линии общей нормали. Тогда по (5.13)  и
и  , т.е. при центральном ударе угловые скорости шаров не изменяются.
, т.е. при центральном ударе угловые скорости шаров не изменяются. . Вычислим проекцию этой скорости на ось
. Вычислим проекцию этой скорости на ось 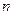 как
как .
.
 .
.

 скоростей центов шаров позволяет записать соотношения
скоростей центов шаров позволяет записать соотношения и
и  , где
, где  и
и  - значения углов
- значения углов  а
а  . Перепишем проекции на ось
. Перепишем проекции на ось  ;
; .
.
 .
.