 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Теорема об изменении кинетического момента относительно неподвижного центра. Дифференциальное уравнение вращения твердого тела относительно неподвижной оси
2.4.1. Кинетический момент механической системы. Момент количества движения материальной точки относительно выбранного центра называется ее кинетическим моментом
здесь
Кинетическим моментом
Проецируя (2.12) на оси неподвижной декартовой системы координат
Для механических систем с непрерывным распределением массы в выражениях (2.12) и (2.13) суммирование следует заменить интегрированием. Кинетический момент системы, вычисленный относительно неподвижного центра О (его проекция на ось, проходящую через точку О), является векторной мерой, характеризующей вращение механической системы относительно неподвижного центра (оси). В качестве примера вычислим кинетический момент тела при его вращении вокруг неподвижной точки и вокруг неподвижной оси. Выделим в твердом теле в окрестности точки, положение которой определяется радиусом – вектором Тогда кинетический момент
В декартовой координатной системе
В сжатом виде это выражение обычно записывают так:
Величины называются моментами инерции тела относительно осей Из шести моментов инерции составляют симметрическую матрицу
которую называют тензором инерции. С помощью тензора
В частном случае, когда тело вращается вокруг неподвижной оси
2.4.2. Теорема об изменении кинетического момента относительно неподвижного центра. Рассмотрим механическую систему из Выражение (2.5) векторно домножим на
Первое слагаемое в правой части представляет собой главный момент
Окончательно получится следующий результат
являющийся математической записью теоремы об изменении кинетического момента механической системы относительно неподвижного центра О: производная по времени от кинетического момента механической системы, вычисленного относительно неподвижного центра, равна главному моменту внешних сил относительно этого центра. Проецируя (2.19) на оси декартовой координатной системы
Из формулы (2.19) следует, что если главный момент внешних сил окажется равным нулю, то на рассматриваемом интервале времени кинетический момент механической системы не изменяется. Если окажется, что равна нулю проекция на какую-либо координатную ось главного момента внешних сил, то будет постоянной проекция на эту ось вектора кинетического момента механической системы. ПРИМЕР 2.4 (задача 37.58 из [2]). Тележка поворотного подъемного крана движется с постоянной скоростью
Мотор, вращающий кран, создает в период разгона постоянный момент, равный Определить угловую скорость РЕШЕНИЕ. Рассмотрим механическую систему, состоящую из поворотного крана и тележки. Внешними усилиями, действующими на нее, являются силы веса, силы реакций в опорных подшипниках А и В, момент Составим для рассматриваемой механической системы последнее выражение из (2.20):
Разделим переменные и выполним интегрирование. Тогда
Составим выражение для кинетического момента системы
2.4.3. Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси.Пусть твердое тело вращается вокруг неподвижной оси
где ПРИМЕР 2.5 (задача 37.9 из [2]). Шарик А, находящийся в сосуде с жидкостью и прикрепленный к концу стержня АВ длины
Сила сопротивления жидкости пропорциональна угловой скорости вращения: РЕШЕНИЕ. Рассмотрим твердое тело в виде оси СD и стержня АВ , масса
Разделим переменные и возьмем от обеих частей равенства определенные интегралы
Окончательно для искомого промежутка времени получим выражение
Для нахождения сделанного числа оборотов вернемся к исходному дифференциальному уравнению. Выполним замену переменных, умножив и разделив его левую часть на
Разделим переменные и возьмем определенные интегралы от обеих частей равенства:
Окончательно для числа оборотов получим выражение
Заметим, что ход решения не отличается от выполненного в примере 1.2.
Поиск по сайту: |
 , (2.11)
, (2.11)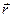 - радиус – вектор точки относительно неподвижного центра О.
- радиус – вектор точки относительно неподвижного центра О.
 механической системы относительно центра О называется геометрическая сумма (главный момент) количеств движения составляющих эту систему материальных точек относительно этого же центра О:
механической системы относительно центра О называется геометрическая сумма (главный момент) количеств движения составляющих эту систему материальных точек относительно этого же центра О: . (2.12)
. (2.12) , получим выражения для соответствующих проекций (иногда их называют моментами количеств движения относительно соответствующих осей):
, получим выражения для соответствующих проекций (иногда их называют моментами количеств движения относительно соответствующих осей): ;
;
 (2.13)
(2.13) .
. , масса которого
, масса которого  так же элементарна (
так же элементарна (  - плотность материала в окрестности выбранной точки).
- плотность материала в окрестности выбранной точки). . (2.14)
. (2.14)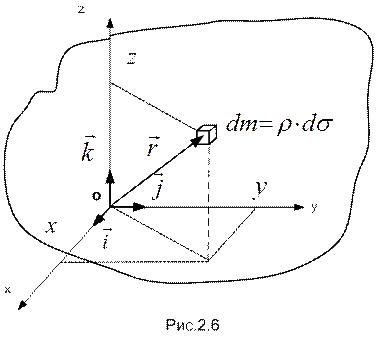
 . Если теперь применить правило векторного перемножения
. Если теперь применить правило векторного перемножения , то для кинетического момента
, то для кинетического момента  (2.15)
(2.15) (2.16)
(2.16) ;
;  ;
; 
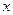 ,
, 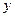 и
и 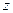 , соответственно, а
, соответственно, а  ,
,  ,
,  - центробежными моментами инерции твердого тела. Все эти величины характеризуют инерционные свойства тела при вращении. Они являются характеристиками распределения массы в твердом теле. Для однородных тел, у которых плотность
- центробежными моментами инерции твердого тела. Все эти величины характеризуют инерционные свойства тела при вращении. Они являются характеристиками распределения массы в твердом теле. Для однородных тел, у которых плотность  ,
, компоненты
компоненты  вектора
вектора  выражаются через компоненты
выражаются через компоненты  вектора
вектора  в очень простой форме:
в очень простой форме: . (2.17)
. (2.17) и
и 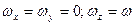 , кинетический момент тела определяется выражением
, кинетический момент тела определяется выражением . (2.18)
. (2.18)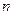 материальных точек с массами
материальных точек с массами 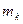 , радиусы – векторы, скорости и ускорения которых в инерциальной системе отсчета с центром О равны
, радиусы – векторы, скорости и ускорения которых в инерциальной системе отсчета с центром О равны  ,
,  и
и  ,
,  , соответственно.
, соответственно. и просуммируем для всех точек механической системы. Получим
и просуммируем для всех точек механической системы. Получим .
. внешних сил, действующих на точки механической системы, вычисленный относительно неподвижного центра О. Второе слагаемое
внешних сил, действующих на точки механической системы, вычисленный относительно неподвижного центра О. Второе слагаемое  было рассмотрено выше; оно представляет собой равный нулю главный момент внутренних сил. Стоящая в левой части равенства сумма преобразуется к виду
было рассмотрено выше; оно представляет собой равный нулю главный момент внутренних сил. Стоящая в левой части равенства сумма преобразуется к виду .
. , (2.19)
, (2.19)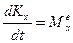 ,
,  ,
,  . (2.20)
. (2.20) относительно стрелы (см. рис.2.7).
относительно стрелы (см. рис.2.7).
 .
. вращения крана в зависимости от расстояния
вращения крана в зависимости от расстояния 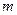 ,
, 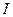 - момент инерции крана (без тележки) относительно оси вращения; вращение начинается в момент, когда тележка находилась на расстоянии
- момент инерции крана (без тележки) относительно оси вращения; вращение начинается в момент, когда тележка находилась на расстоянии  от оси АВ.
от оси АВ. .
. , где
, где  .
. , выразим время
, выразим время  через скорость движения тележки
через скорость движения тележки  и учтем эти выражения в результатах интегрирования. Окончательно получим
и учтем эти выражения в результатах интегрирования. Окончательно получим .
. задан. Из (2.18) найдем проекцию вектора кинетического момента на ось вращения
задан. Из (2.18) найдем проекцию вектора кинетического момента на ось вращения  и подставим ее в третье уравнение из (2.20). Окончательно имеем:
и подставим ее в третье уравнение из (2.20). Окончательно имеем: или
или  , (2.21)
, (2.21) и
и  , приводится во вращение вокруг вертикальной оси СD с начальной угловой скоростью
, приводится во вращение вокруг вертикальной оси СD с начальной угловой скоростью  (см. рис.2.8).
(см. рис.2.8).
 , где
, где 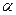 - коэффициент пропорциональности. Определить, через какой промежуток времени угловая скорость вращения станет в два раза меньше начальной, а так же число оборотов
- коэффициент пропорциональности. Определить, через какой промежуток времени угловая скорость вращения станет в два раза меньше начальной, а так же число оборотов  . Заметим, что момент относительно оси вращения создает только сила сопротивления. Запишем для рассматриваемого тела дифференциальное уравнение вращательного движения:
. Заметим, что момент относительно оси вращения создает только сила сопротивления. Запишем для рассматриваемого тела дифференциальное уравнение вращательного движения: .
. .
. .
. .
. .
. .
. .
.