 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Введение в динамику механической системы
Механической системой называют любую выделенную для анализа совокупность материальных точек. Такой системой является, в частности, твердое тело, если рассматривать его как совокупность достаточно малых частиц, на которые это тело может быть мысленно разделено при сохранении основных свойств тела в каждой из этих частиц. Так же, как и в случае твердого тела, принято разделять механические системы на свободные и несвободные. Механическая система называется несвободной, если извне на нее наложены внешние связи. Наличие внутренних связей здесь не оговаривается – они могут быть, а могут и отсутствовать. К этому типу механических систем относятся, например, практически все механизмы и машины. Свободные механические системы – это системы, на которые внешние связи не наложены. Примерами таких систем являются летящие самолеты и ракеты, а так же подводные лодки и глубоководные аппараты в погруженном положении. Принцип освобождения от связей позволяет считать свободной любую несвободную систему; представив систему в виде совокупности взаимодействующих частей, можно каждую из этих частей, в свою очередь, считать свободной механической системой. Последовательно увеличивая число частей, в конце концов, любую механическую систему можно свести к системе свободных материальных точек. При анализе механической системы полезно разделить силы, действующие на любую Внешними называют силы, действующие на точки механической системы со стороны тех точек или тел, которые в нее не входят. Внутренними называют силы взаимодействия между точками, входящими в состав рассматриваемой механической системы. На рис.2.1 показаны силы взаимодействия
Отсюда следует первое свойство внутренних сил – равенство нулю главного вектора
Вычислим также главный момент
Последнее произведение векторов в (2.3) равно нулю, так как они коллинеарны ( Из условия (2.3) следует второе важное свойство внутренних сил – равенство нулю главного момента этих сил относительно произвольно выбранного центра приведения.
Поиск по сайту: |
 -ю точку, на внешние и внутренние.
-ю точку, на внешние и внутренние. и
и  между точками
между точками  и
и  . (2.1)
. (2.1)
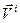 внутренних сил для любой механической системы, т.е.
внутренних сил для любой механической системы, т.е. , где
, где  . (2.2)
. (2.2) относительно произвольно выбранного центра О, создаваемый внутренними силами
относительно произвольно выбранного центра О, создаваемый внутренними силами  . (2.3)
. (2.3) II
II  ).
).